Question

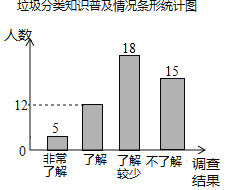
【題目】隨著經濟的快速發展，環境問題越來越受到人們的關注．某校學生會為了了解垃圾分類知識的普及情況，隨機調查了部分學生，調查結果分為“非常了解”“了解”“了解較少”“不了解”四類，并將調查結果繪制成下面兩幅統計圖．

（1）求：本次被調查的學生有多少名？補全條形統計圖．

（2）估計該校1200名學生中“非常了解”與“了解”的人數和是多少．

（3）被調查的“非常了解”的學生中有2名男生，其余為女生，從中隨機抽取2人在全校做垃圾分類知識交流，請利用畫樹狀圖或列表的方法，求恰好抽到一男一女的概率．

Answer 1

【答案】（1）本次被調查的學生有50人，補全圖形見解析；（2）估計該校1200名學生中“非常了解”與“了解”的人數和是408人；（3）恰好抽到一男一女的概率為．

【解析】

（1）由“了解”的人數及其所占百分比求出總人數，總人數乘以對應的百分比可求出“非常了解”、“了解很少”的人數，繼而求出“不了解”的人數，從而補全圖形；
（2）利用樣本估計總體思想求解可得；
（3）畫樹狀圖展示所有20種等可能的結果數，再找出符合條件的結果數，然后利用概率公式求解．

（1）本次被調查的學生有由12÷24%＝50（人），

則“非常了解”的人數為50×10%＝5（人），

“了解很少”的人數為50×36%＝18（人），

“不了解”的人數為50﹣（5+12+18）＝15（人），

補全圖形如下：

（2）估計該校1200名學生中“非常了解”與“了解”的人數和是1200×＝408（人）；

（3）畫樹狀圖為：

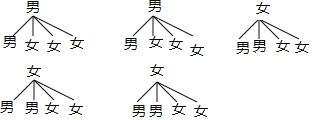
共有20種等可能的結果數，其中恰好抽到一男一女的有12種結果，

所以恰好抽到一男一女的概率為＝．