
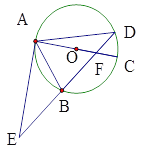
【題目】如圖,已知⊙O的直徑AC與弦BD相交于點F,點E是DB延長線上的一點,∠EAB=∠ADB;
(1)求證:AE是⊙O的切線;
(2)已知點B是EF的中點,求證:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的條件下,求AE的長.
【答案】(1)證明見解析;(2)證明見解析;(3)![]() .
.
【解析】試題分析:(1)、連接CD,根據直徑所對的圓周角為直角得出∠ADB+∠EDC=90°,根據同弧所對的圓周角相等得出∠BAC=∠EDC,然后結合已知條件得出∠EAB+∠BAC=90°,從而說明切線;(2)、連接BC,根據直徑的性質得出∠ABC=90°,根據B是EF的中點得出AB=EF,即∠BAC=∠AFE,則得出三角形相似;(3)、根據三角形相似得出![]() ,根據AF和CF的長度得出AC的長度,然后根據EF=2AB代入
,根據AF和CF的長度得出AC的長度,然后根據EF=2AB代入![]() 求出AB和EF的長度,最后根據Rt△AEF的勾股定理求出AE的長度.
求出AB和EF的長度,最后根據Rt△AEF的勾股定理求出AE的長度.
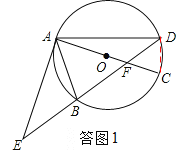
試題解析:(1)、如答圖1,連接CD, ∵AC是⊙O的直徑,∴∠ADC=90°. ∴∠ADB+∠EDC=90°.
∵∠BAC=∠EDC,∠EAB=∠ADB, ∴∠BAC=∠EAB+∠BAC=90°. ∴EA是⊙O的切線.
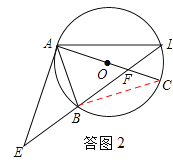
(2)、如答圖2,連接BC, ∵AC是⊙O的直徑,∴∠ABC=90°. ∴∠CBA=∠ABC=90°.
∵B是EF的中點,∴在Rt△EAF中,AB=BF. ∴∠BAC=∠AFE. ∴△EAF∽△CBA.
(3)、∵△EAF∽△CBA,∴![]() . ∵AF=4,CF=2, ∴AC=6,EF=2AB.
. ∵AF=4,CF=2, ∴AC=6,EF=2AB.
∴![]() ,解得AB=2
,解得AB=2![]() .∴EF=4
.∴EF=4![]() .
.
∴AE=![]() .
.


科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.有兩條邊和一個角對應相等的兩個三角形全等
B.矩形的對角線互相垂直平分
C.正方形既是軸對稱圖形又是中心對稱圖形
D.一組對邊平行,另一組對邊相等的四邊形是平行四邊形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在體育課上,九年級2名學生各練習10次立定跳遠,要判斷哪一名學生的成績比較穩定,通常需要比較這2名學生立定跳遠成績的( )
A.方差B.平均數C.頻率分布D.眾數
查看答案和解析>>
科目:初中數學 來源: 題型:
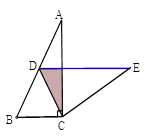
【題目】如圖,在Rt△ABC中,∠A=30°,BC=2,將△ABC繞點C按順時針方向旋轉n度后,得到△EDC,此時點D在AB邊上,斜邊DE交AC于點F,則n=_______; 圖中陰影部分的面積為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠ABC=∠ACB,AD、BD、CD分別平分△ABC的外角∠EAC、內角∠ABC、外角∠ACF.以下結論:① AD∥BC;② ∠ACB=2∠ADB;③ ∠ADC=90°-∠ABD;④ BD平分∠ADC;⑤ 2∠BDC=∠BAC.其中正確的結論有 ( )
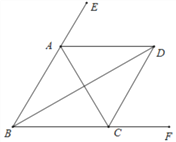
A. ①②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,已知點P(2,1)與點Q(2,﹣1),下列描述正確是( )
A. 關于x軸對稱 B. 關于y軸對稱 C. 關于原點對稱 D. 都在y=2x的圖象上
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將等腰直角三角板放在正方形ABCD的頂點B處,且三角板中BE=EF.連AE,再作EG⊥AE且EG=AE.繞點B旋轉三角板,并保證線段FG與正方形的邊CD交于點H.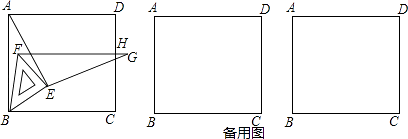
(1)求證:△ABE≌△GFE.
(2)當DH取得最小值時,求∠ABE的度數.
(3)當三角板有兩個頂點在邊BC上時,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com