
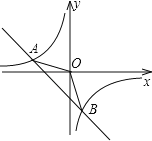
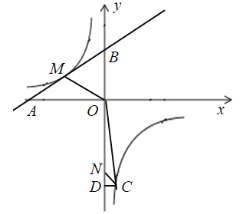
【題目】如圖,已知A(﹣4,n),B(2,﹣4)是一次函數(shù)y=kx+b和反比例函數(shù)y=![]() 的圖象的兩個交點.
的圖象的兩個交點.
(1)求一次函數(shù)和反比例函數(shù)的解析式;
(2)求△AOB的面積.
【答案】(1)y=﹣![]() ,y=﹣x﹣2;(2)6
,y=﹣x﹣2;(2)6
【解析】
(1)把B(2,﹣4)代入反比例函數(shù)y=![]() ,得出m的值,再把A(﹣4,n)代入反比例函數(shù)解析式求出n;將A,B的坐標(biāo)代入一次函數(shù)解析式y=kx+b,運用待定系數(shù)法即可求其解析式;
,得出m的值,再把A(﹣4,n)代入反比例函數(shù)解析式求出n;將A,B的坐標(biāo)代入一次函數(shù)解析式y=kx+b,運用待定系數(shù)法即可求其解析式;
(2)設(shè)直線AB與y軸交于點C,把三角形AOB的面積看成是三角形AOC和三角形OCB的面積之和進行計算.
解:(1)∵B(2,﹣4)在y=![]() 圖象上,
圖象上,
∴m=﹣8.
∴反比例函數(shù)的解析式為y=﹣![]() ;
;
∵點A(﹣4,n)在y=﹣![]() 圖象上,
圖象上,
∴n=2,
∴A(﹣4,2).
∵一次函數(shù)y=kx+b圖象經(jīng)過A(﹣4,2),B(2,﹣4),
∴![]() ,解得
,解得![]() .
.
∴一次函數(shù)的解析式為y=﹣x﹣2;
(2)設(shè)一次函數(shù)y=﹣x﹣2的圖象與y軸交于C點,
當(dāng)x=0時,y=﹣2,
∴點C(0,﹣2).
∴OC=2,
∴S△AOB=S△ACO+S△BCO=![]() ×2×4+
×2×4+![]() ×2×2=6.
×2×2=6.
即△AOB的面積為6.


科目:初中數(shù)學(xué) 來源: 題型:
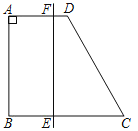
【題目】 如圖,在四邊形ABCD中,AB⊥AD,AD∥BC,且AB=BC=4,AD=2,點E是邊BC上的一個動點,EF⊥BC交AD于點F,將四邊形ABCD沿EF所在直線折疊,若兩邊重疊部分的面積為3,則BE的長為( )
A.![]() 或
或![]() B.
B.![]() C.
C.![]() D.
D.![]() 或4+
或4+![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某水果店購進一批優(yōu)質(zhì)晚熟芒果,進價為10元/千克,售價不低于15元/千克,且不超過40元/千克,根據(jù)銷售情況發(fā)現(xiàn)該芒果在一天內(nèi)的銷售量y(千克)與該天的售價x(元/千克)之間滿足如表所示的一次函數(shù)關(guān)系:

(1)寫出銷售量y與售價x之間的函數(shù)關(guān)系式;
(2)設(shè)某天銷售這種芒果獲利W元,寫出W與售價x之間的函數(shù)關(guān)系式,并求出當(dāng)售價為多少元時,當(dāng)天的獲利最大,最大利潤是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
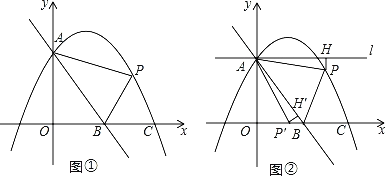
【題目】如圖①,直線AB的解析式為y=﹣![]() x+4,拋物線y=﹣
x+4,拋物線y=﹣![]() +bx+c與y軸交于點A,與x軸交于點C(6,0),點P是拋物線上一動點,設(shè)點P的橫坐標(biāo)為m.
+bx+c與y軸交于點A,與x軸交于點C(6,0),點P是拋物線上一動點,設(shè)點P的橫坐標(biāo)為m.
(1)求拋物線的解析式;
(2)當(dāng)點P在第一象限內(nèi)時,求△ABP面積的最大值,并求此時點P的坐標(biāo);
(3)如圖②,當(dāng)點P在y軸右側(cè)時,過點A作直線l∥x軸,過點P作PH⊥l于點H,將△APH繞點A順時針旋轉(zhuǎn),當(dāng)點H的對應(yīng)點H′恰好落在直線AB上時,點P的對應(yīng)點P′恰好落在坐標(biāo)軸上,請直接寫出點P的橫坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
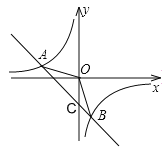
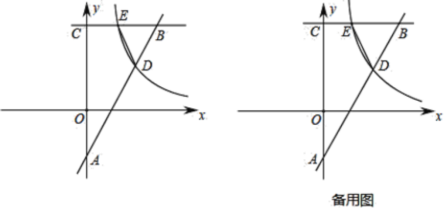
【題目】Rt△OBC在直角坐標(biāo)系內(nèi)的位置如圖所示,點C在y軸上,∠OCB=90°,反比例函數(shù)y=![]() (k>0)在第一象限內(nèi)的圖象與OB邊交于點D(m,3),與BC邊交于點E(n,6).
(k>0)在第一象限內(nèi)的圖象與OB邊交于點D(m,3),與BC邊交于點E(n,6).
(1)求m與n的數(shù)量關(guān)系;
(2)連接CD,若△BCD的面積為12,求反比例函數(shù)的解析式和直線OB的解析式;
(3)設(shè)點P是線段OB邊上的點,在(2)的條件下,是否存在點P,使得以B、C、P為項點的三角形與△BDE相似?若存在,求出此時點P戶的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
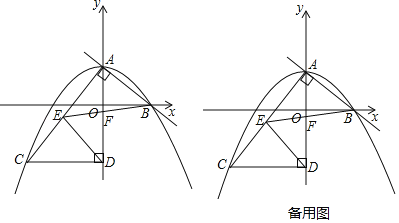
【題目】如圖,在平面直角坐標(biāo)系中,直線y=﹣![]() x+3與y軸交于點A,與x軸交于點B,拋物線y=﹣
x+3與y軸交于點A,與x軸交于點B,拋物線y=﹣![]() x2+bx+c經(jīng)過點A和點B,過點A作AC⊥AB交拋物線于點C,過點C作CD⊥y軸于點D,點E在線段AC上,連接ED,且ED=EC,連接EB交y軸于點F.
x2+bx+c經(jīng)過點A和點B,過點A作AC⊥AB交拋物線于點C,過點C作CD⊥y軸于點D,點E在線段AC上,連接ED,且ED=EC,連接EB交y軸于點F.
(1)求拋物線的表達式;
(2)求點C的坐標(biāo);
(3)若點G在直線AB上,連接FG,當(dāng)∠AGF=∠AFB時,直接寫出線段AG的長;
(4)在(3)的條件下,點H在線段ED上,點P在平面內(nèi),當(dāng)△PAG≌△PDH時,直接寫出點P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
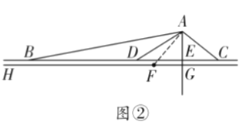
【題目】疫情突發(fā),危難時刻,從決定建造到交付使用,雷神山、火神山醫(yī)院僅用時十天,其建造速度之快,充分展現(xiàn)了中國基建的巨大威力!這樣的速度和動員能力就是全 國人民的堅定信心和盡快控制疫情的底氣!改革開放![]() 年來,中國已經(jīng)成為領(lǐng)先世界的基 建強國,如圖①是建筑工地常見的塔吊,其主體部分的平面示意圖如圖②,點
年來,中國已經(jīng)成為領(lǐng)先世界的基 建強國,如圖①是建筑工地常見的塔吊,其主體部分的平面示意圖如圖②,點![]() 在線段
在線段![]() 上運動,
上運動,![]() 垂足為點
垂足為點![]() 的延長線交
的延長線交![]() 于點
于點 ![]() ,經(jīng)測量
,經(jīng)測量![]()
![]() ,
,

(1)求線段![]() 的長度;(結(jié)果 精確到
的長度;(結(jié)果 精確到![]() )
)
(2)連接![]() ,當(dāng)線段
,當(dāng)線段![]() 時, 求點
時, 求點![]() 和點
和點![]() 之間的距離.(結(jié)果 精確到
之間的距離.(結(jié)果 精確到![]() ,參考數(shù)據(jù):
,參考數(shù)據(jù):![]()
![]() )
)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
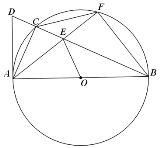
【題目】如圖,△ABC是⊙O內(nèi)接三角形,AB是⊙O的直徑,C是弧AF的中點,弦BC,AF相交于點E,在BC延長線上取點D,使得AD=AE.
(1)求證:AD是⊙O切線;
(2)若∠OEB=45°,求sin∠ABD的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一次函數(shù)![]() 的圖像與
的圖像與![]() 軸分別交于
軸分別交于![]() 兩點,與反比例函數(shù)
兩點,與反比例函數(shù)![]() 的圖像交于點
的圖像交于點![]() ,點C在反比例函數(shù)
,點C在反比例函數(shù)![]() 的圖像上,過點C作
的圖像上,過點C作![]() 軸于點D,連接
軸于點D,連接![]() ,已知
,已知![]() .
.
(1)![]() ,點A的坐標(biāo)為________________.
,點A的坐標(biāo)為________________.
(2)點![]() 在線段
在線段![]() 上,連接
上,連接![]() ,且
,且![]() ,求點C的坐標(biāo).
,求點C的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com