
【題目】如圖,在![]() 中,延長
中,延長![]() 至點
至點![]() ,使
,使![]() ,連接
,連接![]() ,作
,作![]() 于點
于點![]() ,
,![]() 交
交![]() 的延長線于點
的延長線于點![]() ,且
,且![]() .
.

(1)求證:![]() ;
;
(2)如果![]() ,求
,求![]() 的度數(shù).
的度數(shù).
【答案】(1)詳見解析;(2)40°
【解析】
(1)先由HL判定Rt△BCE≌Rt△CDF,得到∠ABC=∠DCF,然后由對頂角相等可得:∠DCF=∠ACB,進而可得∠ABC=∠ACB,然后由等角對等邊,可得AB=AC;
(2)由CD=BC,可得∠CBD=∠CDB,然后由三角形的外角的性質可得:∠ACB=∠CBD+∠CDB=2∠CBD,由∠ABC=∠ACB,進而可得:∠ABC=2∠CBD,然后由∠ABD=∠ABC+∠CBD=3∠CBD=105![]() ,進而可求:∠CBD的度數(shù)及∠ABC的度數(shù),然后由三角形的內角和定理即可求∠A的度數(shù).
,進而可求:∠CBD的度數(shù)及∠ABC的度數(shù),然后由三角形的內角和定理即可求∠A的度數(shù).
解:(1)證明:∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學 來源: 題型:
【題目】閱讀材料(1),并利用(1)的結論解決問題(2)和問題(3).
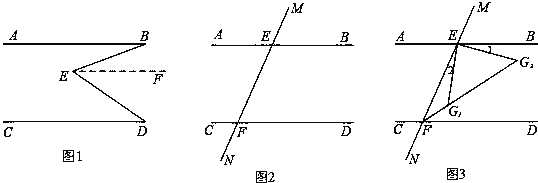
(1)如圖1,AB∥CD,E為形內一點,連結BE、DE得到∠BED,求證:∠E=∠B+∠D
悅悅是這樣做的:
過點E作EF∥AB.則有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.
(2)如圖2,畫出∠BEF和∠EFD的平分線,兩線交于點G,猜想∠G的度數(shù),并證明你的猜想.
(3)如圖3,EG1和EG2為∠BEF內滿足∠1=∠2的兩條線,分別與∠EFD的平分線交于點G1和G2,求證:∠FG1E+∠G2=180°.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
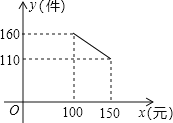
【題目】為發(fā)展“低碳經濟”,某單位花12500引進了一條環(huán)保型生產線生產新產品,在生產過程中,每件產品還需成本40元,物價部門規(guī)定該產品售價不得低于100元/件且不得高于150元/件,每月銷售量y(件)與銷售單價x(元)之間的函數(shù)關系如圖所示:
(1)求y與x之間的函數(shù)關系式,并寫出x的取值范圍;
(2)第一個月該單位是盈利還是虧損?求出當盈利最大或虧損最小時的產品售價;
(3)在(2)的前提下,即在第一個月盈利最大或虧損最小時,第二個月公司重新確定產品售價,能否使兩個月共盈利達10800元?若能,求出第二個月的產品售價;若不能,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,等腰三角形![]() 的底邊
的底邊![]() 長為
長為![]() ,面積是
,面積是![]() , 腰
, 腰![]() 的垂直平分線
的垂直平分線![]() 分別交
分別交![]() 邊于
邊于![]() 點.若點
點.若點![]() 為
為![]() 邊的中點,點
邊的中點,點![]() 為線段EF上一動點,則
為線段EF上一動點,則![]() 周長的最小值為( )
周長的最小值為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,點
厘米,點![]() 為
為![]() 的中點.
的中點.
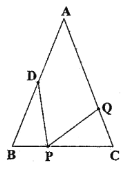
(1)如果點![]() 在線段
在線段![]() 上以
上以![]() 厘米
厘米![]() 秒的速度由
秒的速度由![]() 向
向![]() 點運動,同時點
點運動,同時點![]() 在線段
在線段![]() 上由
上由![]() 點向
點向![]() 點運動.
點運動.
①若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度相等,
的運動速度相等,![]() 秒鐘時,
秒鐘時,![]() 與
與![]() 是否全等?請說明理由;
是否全等?請說明理由;
②點![]() 的運動速度與點
的運動速度與點![]() 的運動速度不相等,當點
的運動速度不相等,當點![]() 的運動速度為多少時,能夠使
的運動速度為多少時,能夠使![]() ?并說明理由;
?并說明理由;
(2)若點![]() 以②中的運動速度從點
以②中的運動速度從點![]() 出發(fā),點
出發(fā),點![]() 以原來運動速度從點
以原來運動速度從點![]() 同時出發(fā),都逆時針沿
同時出發(fā),都逆時針沿![]() 的三邊運動,求多長時間點
的三邊運動,求多長時間點![]() 與點
與點![]() 第一次在
第一次在![]() 的哪條邊上相遇?
的哪條邊上相遇?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,若A(﹣4,n),B(2,﹣4)是一次函數(shù)y=kx+b的圖象和反比例函數(shù)y=![]() 的圖象的兩個交點.
的圖象的兩個交點.
(1)求反比例函數(shù)和一次函數(shù)的解析式;
(2)求直線AB與x軸的交點C的坐標及△AOB的面積;
(3)觀察圖象,直接寫出反比例函數(shù)值大于一次函數(shù)值x取值范圍.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
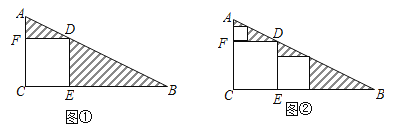
【題目】三角形紙片ABC中,∠C=90°,AC=1,BC=2.按圖①的方式在這張紙片中剪去一個盡可能大的正方形,稱為第1次剪取,記余下的兩個三角形面積和為S1;按圖②的方式在余下的Rt△ADF和Rt△BDE中,分別剪去盡可能大的正方形,稱為第2次剪取,記余下的兩個三角形面積和為S2;繼續(xù)操作下去…….
(1)如圖①,求![]() 和S1的值;
和S1的值;
(2)第n次剪取后,余下的所有三角形面積之和Sn為________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某養(yǎng)殖戶的養(yǎng)殖成本逐年增長,第一年的養(yǎng)殖成本為12萬元,第3年的養(yǎng)殖成本為16萬元.設養(yǎng)殖成本平均每年增長的百分率為x,則下面所列方程中正確的是( )
A. 12(1﹣x)2=16 B. 16(1﹣x)2=12 C. 16(1+x)2=12 D. 12(1+x)2=16
【答案】D
【解析】由題意可得:第二年的養(yǎng)殖成本為![]() ,
,
第三年的養(yǎng)殖成本為: ![]() ,
,
∴![]() .
.
故選D.
【題型】單選題
【結束】
8
【題目】一個布袋內只裝有1個黑球和2個白球,這些球除顏色外其余都相同,隨機摸出一個球后放回并攪勻,再隨機摸出一個球,則兩次摸出的球都是黑球的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com