
【題目】在△ABC中,AB=AC,∠BAC=α,點P是△ABC內一點,且∠PAC+∠PCA=![]() ,連接PB,試探究PA、PB、PC滿足的等量關系.
,連接PB,試探究PA、PB、PC滿足的等量關系.
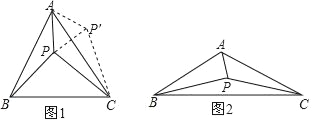
(1)當α=60°時,將△ABP繞點A逆時針旋轉60°得到△ACP′,連接PP′,如圖1所示.由△ABP≌△ACP′可以證得△APP′是等邊三角形,再由∠PAC+∠PCA=30°可得∠APC的大小為 度,進而得到△CPP′是直角三角形,這樣可以得到PA、PB、PC滿足的等量關系為 ;
(2)如圖2,當α=120°時,參考(1)中的方法,探究PA、PB、PC滿足的等量關系,并給出證明;
(3)PA、PB、PC滿足的等量關系為 .
【答案】(1)150,PA2+PC2=PB2;(2)3PA2+PC2=PB2;(3)4PA2sin2![]() +PC2=PB2
+PC2=PB2
【解析】試題分析:(1)根據旋轉變換的性質得到△PAP′為等邊三角形,得到∠P′PC=90°,根據勾股定理解答即可;
(2)如圖2,作將△ABP繞點A逆時針旋轉120°得到△ACP′,連接PP′,作AD⊥PP′于D,根據余弦的定義得到PP′=![]() PA,根據勾股定理解答即可;
PA,根據勾股定理解答即可;
(3)與(2)類似,根據旋轉變換的性質、勾股定理和余弦、正弦的關系計算即可.
試題解析:
(1)∵△ABP≌△ACP′,
∴AP=AP′,
由旋轉變換的性質可知,∠PAP′=60°,P′C=PB,
∴△PAP′為等邊三角形,
∴∠APP′=60°,
∵∠PAC+∠PCA=![]() =30°,
=30°,
∴∠APC=150°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∴PA2+PC2=PB2,
故答案為:150,PA2+PC2=PB2;
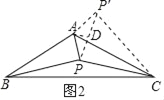
(2)如圖2,作將△ABP繞點A逆時針旋轉120°得到△ACP′,連接PP′,
作AD⊥PP′于D,
由旋轉變換的性質可知,∠PAP′=120°,P′C=PB,
∴∠APP′=30°,
∵∵∠PAC+∠PCA=![]() =60°,
=60°,
∴∠APC=120°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=30°,
∴PD=![]() PA,
PA,
∴PP′=![]() PA,
PA,
∴3PA2+PC2=PB2;
(3)如圖2,與(2)的方法類似,
作將△ABP繞點A逆時針旋轉α得到△ACP′,連接PP′,
作AD⊥PP′于D,
由旋轉變換的性質可知,∠PAP′=α,P′C=PB,
∴∠APP′=90°﹣![]() ,
,
∵∵∠PAC+∠PCA=![]() ,
,
∴∠APC=180°﹣![]() ,
,
∴∠P′PC=(180°﹣![]() )﹣(90°﹣
)﹣(90°﹣![]() )=90°,
)=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=90°﹣![]() ,
,
∴PD=PAcos(90°﹣![]() )=PAsin
)=PAsin![]() ,
,
∴PP′=2PAsin![]() ,
,
∴4PA2sin2![]() +PC2=PB2,
+PC2=PB2,
故答案為:4PA2sin2![]() +PC2=PB2.
+PC2=PB2.


科目:初中數學 來源: 題型:
【題目】某學校為使學生及時穿上合身的校服,現提前對該校八年級四班學生即將所穿校服型號情況進行了摸底調查,并根據調查結果繪制了如圖兩個不完整的統計圖(校服型號以身高作為標準,共分為 6 個型號)

根據以上信息,解答下列問題(請寫出每個空所需的求解步驟)
(1)該班共有多少名學生?其中穿 175 型號校服的學生有多少?
(2)在條形統計圖中,請把空缺部分補充完整;(提醒:有兩處需要補充)
(3)在扇形統計圖中,185 型校服所對應的扇形圓心角的大小是 度;
(4)該班學生所穿校服型號的眾數是 型,中位數是 型。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校辦公樓前有一長為![]() ,寬為
,寬為![]() 的長方形空地,在中心位置留出一個半徑為
的長方形空地,在中心位置留出一個半徑為![]() 的圓形區域建一個噴泉,兩邊是兩塊長方形的休息區,陰影部分為綠地.
的圓形區域建一個噴泉,兩邊是兩塊長方形的休息區,陰影部分為綠地.

(1)用含字母和![]() 的式子表示陰影部分的面積;
的式子表示陰影部分的面積;
(2)當![]() =4,
=4,![]() =3,
=3,![]() =1,
=1,![]() =2時,陰影部分面積是多少?(
=2時,陰影部分面積是多少?(![]() 取3)
取3)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,數軸上的A、B兩點所表示的數分別為a、b,a+b<0,ab<0.

(1)原點O的位置在
A.點A的右邊
B.點B的左邊
C.點A與點B之間 ,且靠近點A
D.點A與點B之間 ,且靠近點B
(2)若a-b=2,
①利用數軸比較大小,a 1,b -1;(填“>”、“<”或“=”).
②化簡:|a-1|+|b+1|.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:關于x的一元二次方程ax2﹣2(a﹣1)x+a﹣2=0(a>0).
(1)求證:方程有兩個不相等的實數根;
(2)設方程的兩個實數根分別為x1,x2(其中x1>x2).若y是關于a的函數,且y=ax2x1,求這個函數的表達式;
(3)將(2)中所得的函數的圖象在直線a=2的左側部分沿直線a=2翻折,圖象的其余部分保持不變,得到一個新的圖象.請你結合這個新的圖象直接寫出:當關于a的函數y=2a+b的圖象與此圖象有兩個公共點時,b的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
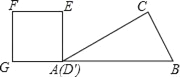
【題目】如圖,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2![]() 為邊長的正方形DEFG的一邊GD在直線AB上,且點D與點A重合,現將正方形DEFG沿A﹣B的方向以每秒1個單位的速度勻速運動,當點D與點B重合時停止,則在這個運動過程中,正方形DEFG與△ABC的重合部分的面積S與運動時間t之間的函數關系圖象大致是( )
為邊長的正方形DEFG的一邊GD在直線AB上,且點D與點A重合,現將正方形DEFG沿A﹣B的方向以每秒1個單位的速度勻速運動,當點D與點B重合時停止,則在這個運動過程中,正方形DEFG與△ABC的重合部分的面積S與運動時間t之間的函數關系圖象大致是( )
A. 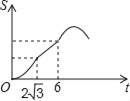 B.
B. 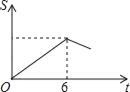 C.
C. 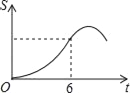 D.
D. 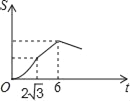
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】線段AB的兩端點的坐標為A(﹣1,0),B(0,﹣2).現請你在坐標軸上找一點P,使得以P、A、B為頂點的三角形是直角三角形,則滿足條件的P點的坐標是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】春節期間,某商場計劃購進甲、乙兩種商品,已知購進甲商品2件和乙商品3件共需270元;購進甲商品3件和乙商品2件共需230元.
(1)求甲、乙兩種商品每件的進價分別是多少元?
(2)商場決定甲商品以每件40元出售,乙商品以每件90元出售,為滿足市場需求,需購進甲、乙兩種商品共100件,且甲種商品的數量不少于乙種商品數量的4倍,請你求出獲利最大的進貨方案,并求出最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知四邊形ABCD是平行四邊形,對角線AC、BD交于點O,E是BC的中點,以下說法錯誤的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com