
【題目】如圖,在△ABC中,AB=AC,⊙O分別切AB于M,BC于N,連接BO、CO,BO=CO.

(1)求證:AC是⊙O的切線;
(2)連接MC,若![]() ,求sin∠B的值.
,求sin∠B的值.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)連接NO,過點O作OE⊥AC于點E,由![]() 可得∠ABC=∠ACB,結合
可得∠ABC=∠ACB,結合![]() ,證明
,證明![]() 利用角平分線的性質可得NO=EO,則結論得證;
利用角平分線的性質可得NO=EO,則結論得證;
(2)過點M作MF⊥BC于點F,連結OM,ON,證得BM=BN=![]() BC,設BC=a,CF=b,則MF=
BC,設BC=a,CF=b,則MF=![]() b,BF=a-b,BM=
b,BF=a-b,BM=![]() a,可得
a,可得![]() ,解方程得b=
,解方程得b=![]() ,可求出答案.
,可求出答案.
(1)證明:如圖1,連接NO,過點O作OE⊥AC于點E,
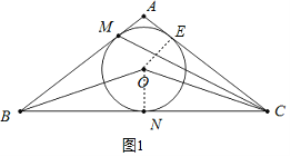
∵AB=AC,
∴∠ABC=∠ACB,
∵⊙O分別切AB于M,BC于N,
![]() ∠ABO=∠CBO,
∠ABO=∠CBO,
![]()
![]()
∴![]()
∵ON⊥BC,OE⊥AC,
∴NO=EO,
∴AC是⊙O的切線;
(2)解:如圖2,過點M作MF⊥BC于點F,連結OM,ON,
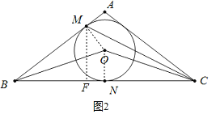
∵OM=ON,OB=OB,![]()
∴Rt△BOM≌Rt△BON(HL),
∴BM=BN,
∵OB=OC,ON⊥BC,
∴BN=CN=![]() BC,
BC,
∴![]()
∵![]()
∴![]() ,
,
∴ ,
,
設BC=a,CF=b,則MF=![]() ,BF=a﹣b,BM=
,BF=a﹣b,BM=![]() ,
,
∵![]()
∴![]() ,
,
解得b=![]() 或b=a(舍去).
或b=a(舍去).
∴


科目:初中數學 來源: 題型:
【題目】如圖,等邊![]() 邊長為
邊長為![]() ,點
,點![]() 是
是![]() 的內心,
的內心,![]() ,繞點
,繞點![]() 旋轉
旋轉![]() ,分別交線段
,分別交線段![]() 、
、![]() 于
于![]() 、
、![]() 兩點,連接
兩點,連接![]() ,給出下列四個結論:①
,給出下列四個結論:①![]() 形狀不變;②
形狀不變;②![]() 的面積最小不會小于四邊形
的面積最小不會小于四邊形![]() 的面積的四分之一;③四邊形
的面積的四分之一;③四邊形![]() 的面積始終不變;④
的面積始終不變;④![]() 周長的最小值為
周長的最小值為![]() .上述結論中正確的個數是( )
.上述結論中正確的個數是( )
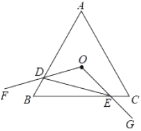
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,菱形ABOC的頂點O在坐標原點,邊BO在x軸的負半軸上,![]() ,頂點C的坐標為
,頂點C的坐標為![]() ,x反比例函數
,x反比例函數![]() 的圖象與菱形對角線AO交于點D,連接BD,當
的圖象與菱形對角線AO交于點D,連接BD,當![]() 軸時,k的值是______.
軸時,k的值是______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,3個正方形在⊙O直徑的同側,頂點B、C、G、H都在⊙O的直徑上,正方形ABCD的頂點A在⊙O上,頂點D在PC上,正方形EFGH的頂點E在⊙O上、頂點F在QG上,正方形PCGQ的頂點P也在⊙O上.若BC=1,GH=2,則CG的長為( )
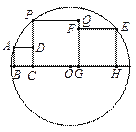
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,BC=6,E為AC邊上的點且AE=2EC,點D在BC邊上且滿足BD=DE,設BD=y,S△ABC=x,則y與x的函數關系式為( )
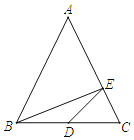
A.y=![]() x2+
x2+![]() B.y=
B.y=![]() x2+
x2+![]()
C.y=![]() x2+2D.y=
x2+2D.y=![]() x2+2
x2+2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,經過點B(﹣2,0)的直線y=kx+b與直線y=4x+2相交于點A(﹣1,﹣2),4x+2<kx+b<0的解集為( )
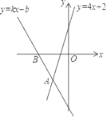
A.x<﹣2B.﹣2<x<﹣1C.x<﹣1D.x>﹣1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分別找一點M,N,使△AMN周長最小時,則∠AMN+∠ANM的度數是________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,y=ax2+bx-2的圖象過A(1,0),B(-2,0),與y軸交于點C.
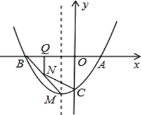
(1)求拋物線關系式及頂點M的坐標;
(2)若N為線段BM上一點,過N作x軸的垂線,垂足為Q,當N在線段BM上運動(N不與點B、點M重合),設NQ的長為t,四邊形NQAC的面積為S,求S與t的關系式并求出S的最大值;
(3)在拋物線的對稱軸上是否存在點P,使△PAC為直角三角形?若存在,請直接寫出所有符合條件P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com