
【題目】“春節”是我國的傳統佳節,民間歷來有吃“湯圓”的習俗.某食品廠為了解市民對去年銷量較好的肉餡(A)、豆沙餡 (B)、菜餡(C)、三丁餡 (D)四種不同口味湯圓的喜愛情況,在節前對某居民區市民進行了抽樣調查,并將調查情況繪制成如下兩幅統計圖(尚不完整).請根據以上信息回答:
(1)本次參加抽樣調查的居民人數是 人;
(2)將圖 ①②補充完整;( 直接補填在圖中)
(3)求圖②中表示“A”的圓心角的度數;
(4)若居民區有8000人,請估計愛吃D湯圓的人數.
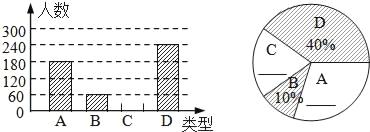
【答案】(1)600;(2)120人,20%;30%;(3)108°(4)愛吃D湯圓的人數約為3200人
【解析】試題分析:
(1)由兩幅統計圖中的信息可知,喜歡B類的有60人,占被調查人數的10%,由此即可計算出被調查的總人數為60÷10%=600(人);
(2)由(1)中所得被調查總人數為600人結合統計圖中已有的數據可得喜歡C類的人數為:600-180-60-240=120(人),喜歡C類的占總人數的百分比為:120÷600×100%=20%,喜歡A類的占總人數的百分比為:180÷600×100%=30%,由此即可將統計圖補充完整;
(3)由(2)中所得數據可得扇形統計圖中A類所對應的圓心角度數為:360°×30%=108°;
(4)由扇形統計圖中的信息:喜歡D類的占總人數的40%可得:8000×40%=3200(人);
試題解析:
(1)本次參加抽樣調查的居民的人數是:60÷10%=600(人);
故答案為:600;
(2)由題意得:C的人數為600﹣(180+60+240)=600﹣480=120(人),C的百分比為120÷600×100%=20%;A的百分比為180÷600×100%=30%;
將兩幅統計圖補充完整如下所示:

(3)根據題意得:360°×30%=108°,
∴圖②中表示“A”的圓心角的度數108°;
(4)8000×40%=3200(人),
即愛吃D湯圓的人數約為3200人.


科目:初中數學 來源: 題型:
【題目】閱讀下面的文字,解答問題:大家知道![]() 是無理數,而無理數是無限不循環小數,因此
是無理數,而無理數是無限不循環小數,因此![]() 的小數部分我們不可能全部地寫出來,于是小明用
的小數部分我們不可能全部地寫出來,于是小明用![]() ﹣1來表示
﹣1來表示![]() 的小數部分,因為
的小數部分,因為![]() 的整數部分是1,將這個數減去其整數部分,差就是小數部分.請解答:
的整數部分是1,將這個數減去其整數部分,差就是小數部分.請解答:
(1)![]() 的整數部分是 ,小數部分是 ;
的整數部分是 ,小數部分是 ;
(2)如果![]() 的小數部分為a,
的小數部分為a,![]() 的整數部分為b,求a+b﹣
的整數部分為b,求a+b﹣![]() 的值;
的值;
(3)已知:10+![]() =x+y,其中x是整數,且0<y<1,求x﹣y的相反數.
=x+y,其中x是整數,且0<y<1,求x﹣y的相反數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】勾股定理神秘而美妙,它的證法多樣,其巧妙各有不同,其中的“面積法”給了小聰以靈感,他驚喜的發現,當兩個全等的直角三角形如圖1或圖2擺放時,都可以用“面積法”來證明,下面是小聰利用圖1證明勾股定理的過程:
將兩個全等的直角三角形按圖1所示擺放,其中∠DAB=90°,求證:a2+b2=c2.
證明:連結DB,過點D作BC邊上的高DF,則DF=EC=b﹣a,
∵S四邊形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四邊形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
請參照上述證法,利用圖2完成下面的證明.
將兩個全等的直角三角形按圖2所示擺放,其中∠DAB=90°.求證:a2+b2=c2 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,點E,F分別在邊DC,AB上,DE=BF,把平行四邊形沿直線EF折疊,使得點B,C分別落在B′,C′處,線段EC′與線段AF交于點G,連接DG,B′G.
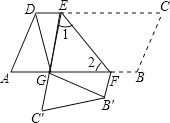
求證:(1)∠1=∠2;
(2)DG=B′G.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,E為CD的中點,連接AE、BE,BE⊥AE,延長AE交BC的延長線于點F.
求證:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目:初中數學 來源: 題型:
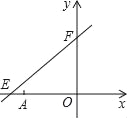
【題目】如圖,直線y=![]() x+6與x軸、y軸分別相交于點E、F,點A的坐標為(﹣6,0),P(x,y)是直線y=
x+6與x軸、y軸分別相交于點E、F,點A的坐標為(﹣6,0),P(x,y)是直線y=![]() x+6上一個動點.
x+6上一個動點.
(1)在點P運動過程中,試寫出△OPA的面積s與x的函數關系式;
(2)當P運動到什么位置,△OPA的面積為![]() ,求出此時點P的坐標;
,求出此時點P的坐標;
(3)過P作EF的垂線分別交x軸、y軸于C、D.是否存在這樣的點P,使△COD≌△FOE?若存在,直接寫出此時點P的坐標(不要求寫解答過程);若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D在⊙O的直徑AB的延長線上,點C在⊙O上,AC=CD,∠ACD=120°.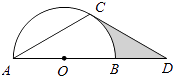
(1)求證:CD是⊙O的切線;
(2)若⊙O的半徑為2,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
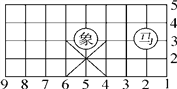
【題目】如圖是中國象棋棋盤的一部分,棋盤中“馬”所在的位置用(2,3)表示.
(1)圖中“象”的位置可表示為____________;
(2)根據象棋的走子規則,“馬”只能從“日”字的一角走到與它相對的另一角;“象”只能從“田”字的一角走到與它相對的另一角.請按此規則分別寫出“馬”和“象”下一步可以到達的位置.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com