
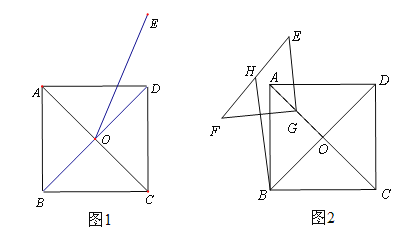
【題目】如圖1,點![]() 為正方形
為正方形![]() 的中心。
的中心。
(1)將線段![]() 繞點
繞點![]() 逆時針方向旋轉
逆時針方向旋轉![]() ,點
,點![]() 的對應點為點
的對應點為點![]() ,連接
,連接![]() ,
, ![]() ,
, ![]() ,請依題意補全圖1;
,請依題意補全圖1;
(2)根據(jù)圖1中補全的圖形,猜想并證明![]() 與
與![]() 的關系;
的關系;
(3)如圖2,點![]() 是
是![]() 中點,△
中點,△![]() 是等腰直角三角形,
是等腰直角三角形, ![]() 是
是![]() 的中點,
的中點, ![]() ,
, ![]() ,
, ![]() ,△
,△![]() 繞
繞![]() 點逆時針方向旋轉
點逆時針方向旋轉![]() 角度,請直接寫出旋轉過程中
角度,請直接寫出旋轉過程中![]() 的最大值。
的最大值。
【答案】(1)圖形見解析(2)證明見解析(3)![]()
【解析】(1)根據(jù)題意畫出圖形即可;
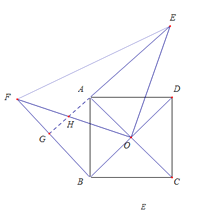
(2)延長EA交OF于點H,交BF于點G,利用正方形的性質和旋轉的性質證明△EOA≌△FOB,得到AE=BF.根據(jù)等邊對等角得到∠OEA=∠OFB,由∠OEA+∠OHA=90°,所以∠OFB+∠FHG=90°,進而得到AE⊥BF.
(3)BH的最大值為![]() .
.
解:(1)正確畫出圖形,如下圖所示:
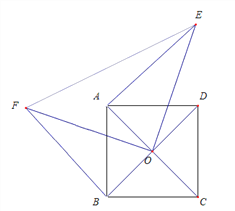
(2)延長EA交OF于點![]() ,交
,交![]() 于點
于點![]()
∵![]() 為正方形
為正方形![]() 的中心,
的中心,
∴![]() ,∠
,∠![]() =90
=90![]() ,
,
∵![]() 繞點
繞點![]() 逆時針旋轉90
逆時針旋轉90![]() 角得到
角得到![]() ,
,
∴![]() ,
,
∴∠![]() =∠
=∠![]() =90
=90![]() ,
,
∴∠![]() =∠
=∠![]() ,
,
在△![]() 和△
和△![]() 中,
中,
 ,
,
∴△![]() ≌△
≌△![]() ,
,
∴![]() ,
,
∴∠![]() =∠
=∠![]() ,
,
∵∠![]() +∠
+∠![]() ,
,
∴∠![]() +∠
+∠![]() =90
=90![]() ,
,
∴![]() ⊥
⊥![]() ;
;
(3)![]() 的最大值為
的最大值為![]() .
.


科目:初中數(shù)學 來源: 題型:
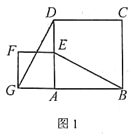
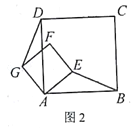
【題目】如圖1,正方形ABCD和正方形AEFG,連接DG,BE。
(1)發(fā)現(xiàn)
當正方形AEFG繞點A旋轉,如圖2,①線段DG與BE之間的數(shù)量關系是____________。②直線DG與直線BE之間的位置關系是____________。
(2)探究
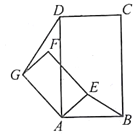
如圖3,若四邊形ABCD與四邊形AEFG都為矩形,且AD=2AB,AG=2AE,證明:直線DG⊥BE
(3)應用
在(2)情況下,連結GE(點E在AB上方),若GE∥AB,且AB=![]() ,AE=1,則線段DG是多少?(直接寫出結論)
,AE=1,則線段DG是多少?(直接寫出結論)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某商店準備進一批小工藝品,每件的成本是40元,經(jīng)市場調查,銷售單價為50元,每天銷售量為100個,若銷售單價每增加1元,銷售量將減少10個.
(1)求每天銷售小工藝品的利潤y(元)和銷售單價x(元)之間的函數(shù)解析式;
(2)商店若準備每天銷售小工藝品獲利960元,則每天銷售多少個?銷售單價定為多少元?
(3)直接寫出銷售單價為多少元時,每天銷售小工藝品的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
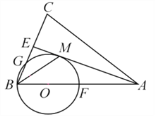
【題目】如圖,在△ABC中,AB=AC,AE是∠BAC的平分線,∠ABC的平分線BM交AE于點M,點O在AB上,以點O為圓心,OB的長為半徑的圓經(jīng)過點M,交BC于點G,交AB于點F.
(1)求證: AE為⊙O的切線;
(2)當BC=8,AC=12時,求⊙O的半徑和BG的長;
(3)在(2)的條件下,求線段BG的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】將連續(xù)的正偶數(shù)2,4,6,8…,排成下表:
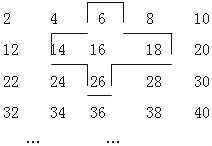
(1)十字框中的五個數(shù)的和是中間的數(shù)16的幾倍?
(2)若將十字框上下左右移動,可框住另外的五個數(shù),設中間的數(shù)為![]() ,用代數(shù)式表示十字框中的五個數(shù)的和;
,用代數(shù)式表示十字框中的五個數(shù)的和;
(3)這五個數(shù)的和能等于2010嗎?如能,寫出這五個數(shù),如不能,說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,OM是∠AOC的平分線,ON是∠BOC的平分線.
(1)如圖1,當∠AOB是直角,∠BOC=60°時,∠MON的度數(shù)是多少?
(2)如圖2,當∠AOB=α,∠BOC=60°時,猜想∠MON與α的數(shù)量關系;
(3)如圖3,當∠AOB=α,∠BOC=β時,猜想∠MON與α、β有數(shù)量關系嗎?如果有,指出結論并說明理由.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,圖(1)中含“○”的矩形有1個,圖(2)中含“○”的矩形有7個,圖(3)中含“○”的矩形有17個,按此規(guī)律,圖(6)中含“○”的矩形有( )
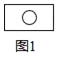
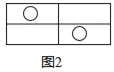
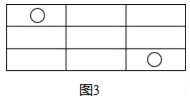
A. 70 B. 71 C. 72 D. 73
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】甲、乙兩人從A地出發(fā)前往B地,甲先出發(fā)1分鐘后,乙再出發(fā),乙出發(fā)一段時間后返回A地取物品,甲、乙兩人同時達到B地和A地,并立即掉頭相向而行直至相遇,甲、乙兩人之間相距的路程y(米)與甲出發(fā)的時間x(分鐘)之間的關系如圖所示,則甲、乙兩人最后相遇時,乙距B地的路程是_____米.
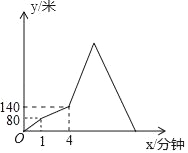
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
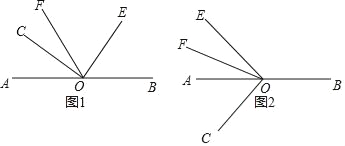
【題目】已知點O是AB上的一點,∠COE=90°,OF平分∠AOE.
(1)如圖1,當點C,E,F在直線AB的同一側時,若∠AOC=40°,求∠BOE和∠COF的度數(shù);
(2)在(1)的條件下,∠BOE和∠COF有什么數(shù)量關系?請直接寫出結論,不必說明理由;
(3)如圖2,當點C,E,F分別在直線AB的兩側時,若∠AOC=β,那么(2)中∠BOE和∠COF的數(shù)量關系是否仍然成立?請寫出結論,并說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com