【題目】如圖，在△ABC中，AD是BC邊上的高，AE是BC邊上的中線，∠C=45°，sinB=
， AD=4．
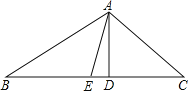
（1）求BC的長；
（2）求tan∠DAE的值．
【答案】（1）
（2）
【解析】
試題（1）先由三角形的高的定義得出∠ADB=∠ADC=90°，再解Rt△ADC，得出DC=4；解Rt△ADB，得出AB=6，根據勾股定理求出BD=2
，然后根據BC=BD+DC即可求解；
（2）先由三角形的中線的定義求出CE的值，則DE=CE-CD，然后在Rt△ADE中根據正切函數的定義即可求解．
試題解析：（1）在△ABC中，∵AD是BC邊上的高，
∴∠ADB=∠ADC=90°．
在△ADC中，∵∠ADC=90°，∠C=45°，AD=4，
∴DC=AD=4．
在△ADB中，∵∠ADB=90°，sinB=
，AD=4，
∴AB=
∴BD=
，
∴BC=BD+DC=
（2）∵AE是BC邊上的中線，
∴CE=
BC=
，
∴DE=CE-CD=
，
∴tan∠DAE=
．
考點: 解直角三角形.
特高級教師點撥系列答案科目：初中數學 來源： 題型：
【題目】如圖，AB為⊙O的直徑，點C為⊙O上一點，將弧BC沿直線BC翻折，使弧BC的中點D恰好與圓心O重合，連接OC，CD，BD，過點C的切線與線段BA的延長線交于點P，連接AD，在PB的另一側作∠MPB=∠ADC．
（1）判斷PM與⊙O的位置關系，并說明理由；
（2）若PC=
，求四邊形OCDB的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有個填寫運算符號的游戲：在“
□
□
□
”中的每個“口”內，填入+，-，×，÷中的某一個（可重復使用），然后計算結果.
（1）計算：
（2）若
口
請推算“口”內的運算符號.
（3）在“□□□”的“口”內填入運算符號后，使計算所得的數最小，直接寫出這個最小的數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，一個點從數軸上的原點開始．先向左移動6cm到達A點，再從A點向右移動10cm到達B點，點C是線段AB的中點．
（1）點C表示的數是 ；
（2）若點A以每秒2cm的速度向左移動，同時C、B兩點分別以每秒1cm、4cm的速度向右移動，設移動時間為t秒，
①運動t秒時，點C表示的數是 （用含有t的代數式表示）；
②當t＝2秒時，CBAC的值為 ．
③試探索：點A、B、C在運動的過程中，線段CB與AC總有怎樣的數量關系？并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某水渠的橫斷面是等腰梯形，已知其斜坡AD的坡度為1：1.2，斜坡BC的坡度為1：0.8，現測得放水前的水面寬EF為3.8米，當水閘放水后，水渠內水面寬GH為6米．則放水后水面上升的高度是（ ）米．
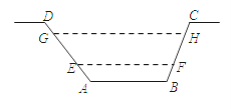
A. 1.2 B. 1.1 C. 0.8 D. 2.2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，菱形ABCD中，AB=2，∠A=120°，點P，Q，K分別為線段BC，CD，BD上的任意一點，則PK+QK的最小值為【 】
A．1 B．
C． 2 D．
＋1
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】材料閱讀：若一個整數能表示成a2＋b2(a、b是正整數)的形式，則稱這個數為“完美數”．例如：因為13＝32＋22，所以13是“完美數”；再如：因為a2＋2ab＋2b2＝(a＋b)2＋b2(a、b是正整數)，所以a2＋2ab＋2b2也是“完美數”．
(1)請你寫出一個大于20小于30的“完美數”，并判斷53是否為“完美數”；
(2)試判斷(x2＋9y2)·(4y2＋x2)(x、y是正整數)是否為“完美數”，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】函數y=
(k＞0)的圖象上兩點A(x1, y1)和B(x2, y2),且x1＞x2＞0，分別過A、B向x軸作AA1⊥x軸于A1，BB1⊥x軸于B1，則
_________
(填“＞”“=”或“＜”)，若
=2，則函數解析式為_________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將長方形ABCD沿直線EF折疊，使頂點C恰好落在頂點A處，已知AB＝4cm，AD＝8cm，則折痕EF的長為( )
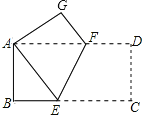
A.5cmB.
cmC.
cmD.
cm
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com