
【題目】在△ABC 中,∠ABC 和∠ACB 的角平分線交于點 M.
(1)若∠ABC=40°,∠ACB=60°,求∠BMC 的度數;
(2)∠BMC 可能是直角嗎?作出判斷,并說明理由.
【答案】(1)130°;(2)∠BMC不可能是直角,理由見詳解
【解析】
(1)根據角平分線的定義可得:∠CBM=20°,∠BCM=30°,最后利用三角形的內角和定理可解答;
(2)同理根據角平分線的定義表示∠CBM+∠BCM,最后根據三角形的內角和表示∠BMC的度數可解答.
解:(1)∵∠ABC和∠ACB的角平分線交于點M,
∴∠CBM=![]() ∠ABC,∠BCM=
∠ABC,∠BCM=![]() ∠ACB,
∠ACB,
∵∠ABC=40°,∠ACB=60°,
∴∠CBM=20°,∠BCM=30°,
∴∠BMC=180°﹣20°﹣30°=130°;
(2)∠BMC不可能是直角,理由如下.
∵∠ABC和∠ACB的角平分線交于點M,
∴∠CBM=![]() ∠ABC,∠BCM=
∠ABC,∠BCM=![]() ∠ACB,
∠ACB,
∴∠CBM+∠BCM=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣![]() ∠A,
∠A,
∴∠BMC=180°﹣(∠CBM+∠BCM)=90°+![]() ∠A,
∠A,
顯然∠BMC>90°.
∴∠BMC不可能是直角.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
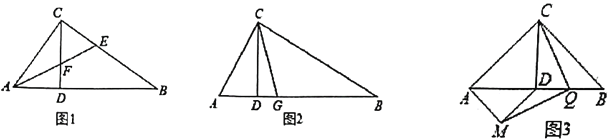
【題目】![]() 是
是![]() 的高.
的高.
(1)如圖1,若![]() ,
,![]() 的平分線
的平分線![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,求證:
,求證:![]() ;
;
(2)如圖2,若![]() ,
,![]() 的平分線
的平分線![]() 交
交![]() 于點
于點![]() ,求
,求![]() 的值;
的值;
(3)如圖3,若![]() 是以
是以![]() 為斜邊的等腰直角三角形,再以
為斜邊的等腰直角三角形,再以![]() 為斜邊作等腰
為斜邊作等腰![]() ,
,![]() 是
是![]() 的中點,連接
的中點,連接![]() 、
、![]() ,試判斷線段
,試判斷線段![]() 與
與![]() 的關系,并給出證明.
的關系,并給出證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,AB=AC,∠A=36°,BD 平分∠ABC 交 AC 于 D,CE 平分∠ACB 交 BD 于 E,圖中 等腰三角形的個數是( )

A.3 個B.4 個C.5 個D.6 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面兩個統計圖反映的是甲、乙兩所學校三個年級的學生在各校學生總人數中的占比情況,下列說法錯誤的是( )
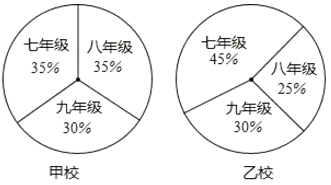
A.甲校中七年級學生和八年級學生人數一樣多B.乙校中七年級學生人數最多
C.乙校中八年級學生比九年級學生人數少D.甲、乙兩校的九年級學生人數一樣多
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小明設計的“分別以兩條已知線段為腰和底邊上的高作等腰三角形”的尺規作圖過程.
已知:線段 a, b.
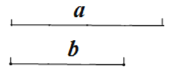
求作:等腰△ABC,使線段 a 為腰,線段 b 為底邊 BC 上的高. 作法:如圖,
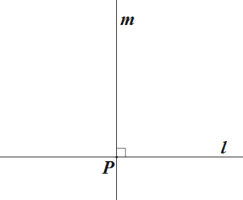
①畫直線 l,作直線 m⊥l,垂足為 P;
②以點 P 為圓心,線段 b 的長為半徑畫弧,交直線 m 于點 A;
③以點 A 為圓心,線段 a 的長為半徑畫弧,交直線 l 于 B,C 兩點;
④分別連接 AB, AC;
所以△ABC 就是所求作的等腰三角形. 根據小明設計的尺規作圖過程,
(1)使用直尺和圓規,補全圖形;(保留作圖痕跡)
(2)完成下面的證明.
證明:∵ = ,
∴△ABC 為等腰三角形( )(填推理的依據).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系 xOy 中,點A,B的坐標分別為(-2,0),(1,0).同時將點A ,B先向左平移1個單位長度,再向上平移2個單位長度,得到點A,B的對應點依次為C,D,連接CD,AC, BD .
(1)寫出點C , D 的坐標;
(2)在 y 軸上是否存在點E,連接EA ,EB,使S△EAB=S四邊形ABDC?若存在,求出點E的坐標;若不存在,說明理由;
(3)點 P 是線段 AC 上的一個動點,連接 BP , DP ,當點 P 在線段 AC 上移動時(不與 A , C 重合),直接寫出CDP 、ABP 與BPD 之間的等量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,連結CE交AD于點F,連結BD交CE于點G,連結BE.下列結論:①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④S四邊形BCDE=![]() BD·CE;⑤BC2+DE2=BE2+CD2.其中正確的結論有( )
BD·CE;⑤BC2+DE2=BE2+CD2.其中正確的結論有( )
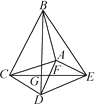
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC.
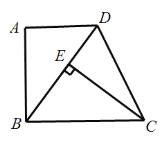
(1)求證:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度數;
(3)若AD=3,AB=4,求DC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com