
【題目】學(xué)習(xí)投影后,小明、小穎利用燈光下自己的影子長(zhǎng)度來(lái)測(cè)量一路燈的高度,并探究影子長(zhǎng)度的變化規(guī)律.如圖,在同一時(shí)間,身高為![]() 的小明
的小明![]() 的影子
的影子![]() 長(zhǎng)是
長(zhǎng)是![]() ,而小穎
,而小穎![]() 剛好在路燈燈泡的正下方
剛好在路燈燈泡的正下方![]() 點(diǎn),并測(cè)得
點(diǎn),并測(cè)得![]() .
.
(1)請(qǐng)?jiān)趫D中畫(huà)出形成影子的光線,并確定路燈燈泡所在的位置![]() ;
;
(2)求路燈燈泡的垂直高度![]() ;
;
(3)如果小明沿線段BH向小穎(點(diǎn)H)走去,當(dāng)小明走到BH中點(diǎn)B1處時(shí),請(qǐng)?jiān)趫D中畫(huà)出此時(shí)小明的影長(zhǎng)B1C1,并求B1C1的長(zhǎng);
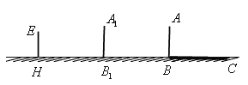
【答案】(1)見(jiàn)解析;(2)路燈燈泡的垂直高度GH是4.8m;(3)小明的影子![]() 的長(zhǎng)是
的長(zhǎng)是![]() m.
m.
【解析】
(1)根據(jù)題意,連接CA,HE并延長(zhǎng)相交于點(diǎn)G,即為所求路燈燈泡的位置,作出圖形即可;
(2)根據(jù)題意得到△ABC∽△GHC ,根據(jù)相似三角形的性質(zhì)得到![]() ,代入即可求出答案,
,代入即可求出答案,
(3)與(2)類似得到△![]() ∽△GH
∽△GH![]() ,根據(jù)相似三角形的性質(zhì)推出
,根據(jù)相似三角形的性質(zhì)推出![]() ,代入即可求出答案,連接G
,代入即可求出答案,連接G![]() 延長(zhǎng)交HC于點(diǎn)
延長(zhǎng)交HC于點(diǎn)![]() ,即得小明的影子.
,即得小明的影子.
(1)如圖,連接CA,HE并延長(zhǎng)相交于點(diǎn)G,即為所求路燈燈泡的位置,作出圖形即可;
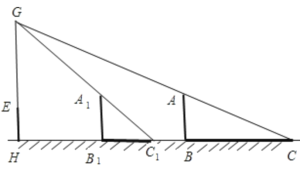
(2)由題意得:易得△ABC∽△GHC,
∴![]() ,
,
∴![]() ,
,
解得:GH=4.8,
答:路燈燈泡的垂直高度GH是4.8m;
故答案為:4.8;
(3)連接G![]() 延長(zhǎng)交HC于點(diǎn)
延長(zhǎng)交HC于點(diǎn)![]() ,則
,則![]()
![]() 即為小明的影子,在(1)中作圖即得,與(2)類似,易證△
即為小明的影子,在(1)中作圖即得,與(2)類似,易證△![]() ∽△GH
∽△GH![]() ,
,
∴![]() ,
,
設(shè)![]() 長(zhǎng)為xm,
長(zhǎng)為xm,![]() 為HB的中點(diǎn),
為HB的中點(diǎn),
則![]() ,
,
解得:x=![]() ,
,
即![]() =
=![]() m,
m,
答:小明的影子![]() 的長(zhǎng)是
的長(zhǎng)是![]() m;
m;
故答案為:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在![]() 中,
中,![]() 于點(diǎn)D.
于點(diǎn)D.
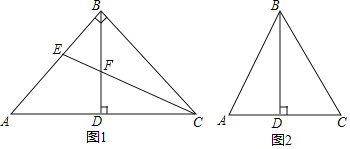
(1)如圖1,當(dāng)![]() 時(shí),若CE平分
時(shí),若CE平分![]() ,交AB于點(diǎn)E,交BD于點(diǎn)F.
,交AB于點(diǎn)E,交BD于點(diǎn)F.
①求證:![]() 是等腰三角形;
是等腰三角形;
②求證:![]() ;
;
(2)點(diǎn)E在AB邊上,連接CE.若![]() ,在圖2中補(bǔ)全圖形,判斷
,在圖2中補(bǔ)全圖形,判斷![]() 與
與![]() 之間的數(shù)量關(guān)系,寫(xiě)出你的結(jié)論,并寫(xiě)出求解
之間的數(shù)量關(guān)系,寫(xiě)出你的結(jié)論,并寫(xiě)出求解![]() 與
與![]() 關(guān)系的思路.
關(guān)系的思路.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】請(qǐng)閱讀下列材料:
問(wèn)題:如圖(1),一圓柱的高為5dm,底面半徑為5dm,BC是底面直徑,求一只螞蟻從A點(diǎn)出發(fā)沿圓柱表面爬行到點(diǎn)C的最短路線.小明設(shè)計(jì)了兩條路線:
路線1:側(cè)面展開(kāi)圖中的AC.如下圖(2)所示:
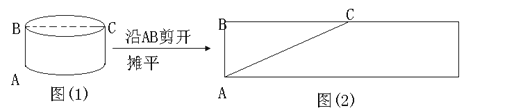
設(shè)路線1的長(zhǎng)度為![]() ,則
,則![]() ,
,
路線2:高線AB + 底面直徑BC.如上圖(1)所示:
設(shè)路線2的長(zhǎng)度為![]() ,則
,則![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
所以要選擇路線2較短.
(1)小明對(duì)上述結(jié)論有些疑惑,于是他把條件改成:“圓柱的底面半徑為1dm,高AB為5dm”繼續(xù)按前面的路線進(jìn)行計(jì)算.請(qǐng)你幫小明完成下面的計(jì)算:
路線1:![]() ___________________;
___________________;
路線2:![]() __________
__________
∵![]()
![]() ,
,
∴![]()
![]() (填>或<) 所以應(yīng)選擇路線_________(填1或2)較短.
(填>或<) 所以應(yīng)選擇路線_________(填1或2)較短.
(2)請(qǐng)你幫小明繼續(xù)研究:在一般情況下,當(dāng)圓柱的底面半徑為r,高為h時(shí),應(yīng)如何選擇上面的兩條路線才能使螞蟻從點(diǎn)A出發(fā)沿圓柱表面爬行到C點(diǎn)的路線最短.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)![]() 為二次函數(shù)
為二次函數(shù)![]() 的圖象的頂點(diǎn).
的圖象的頂點(diǎn).
(1)過(guò)點(diǎn)![]() 作
作![]() 軸的垂線,垂足為點(diǎn)
軸的垂線,垂足為點(diǎn)![]() ,求線段
,求線段![]() 的最小值;
的最小值;
(2)設(shè)正比例函數(shù)![]() 與上述二次函數(shù)的圖象相交于點(diǎn)
與上述二次函數(shù)的圖象相交于點(diǎn)![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時(shí),求
時(shí),求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
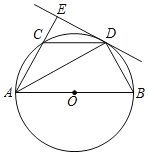
【題目】如圖,AB是⊙O的直徑,C點(diǎn)在⊙O上,AD平分角∠BAC交⊙O于D,過(guò)D作直線AC的垂線,交AC的延長(zhǎng)線于E,連接BD,CD.
(1)求證:BD=CD;
(2)求證:直線DE是⊙O的切線;
(3)若DE=![]() ,AB=4,求AD的長(zhǎng).
,AB=4,求AD的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是李老師在黑板上演示的尺規(guī)作圖及其步驟,
已知鈍角![]() ,尺規(guī)作圖及步驟如下:
,尺規(guī)作圖及步驟如下:
步驟一:以點(diǎn)![]() 為圓心,
為圓心,![]() 為半徑畫(huà)弧;
為半徑畫(huà)弧;
步驟二:以點(diǎn)![]() 為圓心,
為圓心,![]() 為半徑畫(huà)弧,兩弧交于點(diǎn)
為半徑畫(huà)弧,兩弧交于點(diǎn)![]() ;
;
步驟三:連接![]() ,交
,交![]() 延長(zhǎng)線于點(diǎn)
延長(zhǎng)線于點(diǎn)![]() .
.

下面是四位同學(xué)對(duì)其做出的判斷:
小明說(shuō):![]() ;
;
小華說(shuō):![]() ;
;
小強(qiáng)說(shuō):![]() ;
;
小方說(shuō):![]() .
.
則下列說(shuō)法正確的是( )
A.只有小明說(shuō)得對(duì)B.小華和小強(qiáng)說(shuō)的都對(duì)
C.小強(qiáng)和小方說(shuō)的都不對(duì)D.小明和小方說(shuō)的都對(duì)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在菱形![]() 中,對(duì)角線
中,對(duì)角線![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是對(duì)角線
是對(duì)角線![]() 上一點(diǎn)(可與
上一點(diǎn)(可與![]() ,
,![]() 重合),以點(diǎn)
重合),以點(diǎn)![]() 為圓心,
為圓心,![]() 為半徑作
為半徑作![]() (其中
(其中![]() ).
).
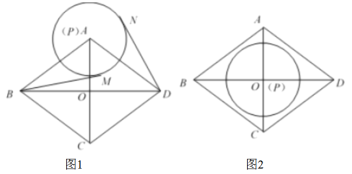
(1)如圖1,當(dāng)點(diǎn)![]() 與
與![]() 重合,且
重合,且![]() 時(shí),過(guò)點(diǎn)
時(shí),過(guò)點(diǎn)![]() ,
,![]() 分別作
分別作![]() 的切線,切點(diǎn)分別為
的切線,切點(diǎn)分別為![]() ,
,![]() .求證:
.求證:![]() ;
;
(2)如圖2,當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合,且
重合,且![]() 在菱形
在菱形![]() 內(nèi)部時(shí)(不含邊界),求
內(nèi)部時(shí)(不含邊界),求![]() 的取值范圍;
的取值范圍;
(3)當(dāng)點(diǎn)![]() 為
為![]() 或
或![]() 的內(nèi)心時(shí),直接寫(xiě)出
的內(nèi)心時(shí),直接寫(xiě)出![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知直線y=kx+b交x軸于點(diǎn)A(1,0) ,與雙曲線![]() 交于點(diǎn)
交于點(diǎn)![]()
(1)求直線AB的解析式為____ ____________;
(2)若 x 軸上存在動(dòng)點(diǎn) M(m,0),過(guò)點(diǎn) M 且與 x 軸垂直的直線與直線AB交于點(diǎn)C,與雙曲線交于點(diǎn)D(C、D兩點(diǎn)不重合),當(dāng)BC >BD時(shí),寫(xiě)出m的取值范圍_____________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
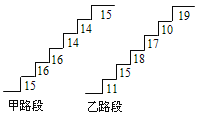
【題目】在某旅游景區(qū)上山的一條小路上,有一些斷斷續(xù)續(xù)的臺(tái)階,下圖是其中的甲、乙兩段臺(tái)階的示意圖,圖中的數(shù)字表示每一級(jí)臺(tái)階的高度(單位:cm).請(qǐng)你用所學(xué)過(guò)的有關(guān)統(tǒng)計(jì)知識(shí),回答下列問(wèn)題(數(shù)據(jù):15,16,16,14,14,15的方差![]() ,數(shù)據(jù):11,15,18,17,10,19的方差
,數(shù)據(jù):11,15,18,17,10,19的方差![]() :
:
(1)分別求甲、乙兩段臺(tái)階的高度平均數(shù);
(2)哪段臺(tái)階走起來(lái)更舒服?與哪個(gè)數(shù)據(jù)(平均數(shù)、中位數(shù)、方差和極差)有關(guān)?
(3)為方便游客行走,需要陳欣整修上山的小路,對(duì)于這兩段臺(tái)階路.在總高度及臺(tái)階數(shù)不變的情況下,請(qǐng)你提出合理的整修建議.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com