
【題目】實(shí)踐探究題
(1)觀察下列有規(guī)律的數(shù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …根據(jù)規(guī)律可知
…根據(jù)規(guī)律可知
①第10個數(shù)是________; ![]() 是第________個數(shù).
是第________個數(shù).
②計(jì)算![]() ________.(直接寫出答案即可)
________.(直接寫出答案即可)
(2)![]() 是不為1的有理數(shù),我們把
是不為1的有理數(shù),我們把![]() 稱為
稱為![]() 的差倒數(shù).如:2的差倒數(shù)是
的差倒數(shù).如:2的差倒數(shù)是![]() ,
,![]() 的差倒數(shù)是
的差倒數(shù)是![]() .已知
.已知![]() ,
,![]() 是
是![]() 的差倒數(shù),
的差倒數(shù),![]() 是
是![]() 的差倒數(shù),
的差倒數(shù),![]() 是
是![]() 的差倒數(shù),…,依此類推,
的差倒數(shù),…,依此類推,![]() 是
是![]() 的差倒數(shù),則
的差倒數(shù),則![]() ________.
________.
(3)高斯函數(shù)[x],也稱為取整函數(shù),即[x]表示不超過x的最大整數(shù).
例如:[2.3]=2,[-1.5]=-2.則下列結(jié)論:①[-2.1]+[1]=-2; ②[x]+[-x]=0
【答案】(1)①![]() ;17;②
;17;②![]() ;(2)4;(3)①③
;(2)4;(3)①③
【解析】
(1)①以上分子均為1,分母是序數(shù)與序數(shù)加1的乘積,據(jù)此可得;由規(guī)律可知第n個數(shù)為![]() ,列方程求解可得;
,列方程求解可得;
②![]() 列項(xiàng)相消求解可得.
列項(xiàng)相消求解可得.
(2)根據(jù)差倒數(shù)定義,經(jīng)過計(jì)算,尋找差倒數(shù)出現(xiàn)的規(guī)律,依據(jù)規(guī)律答題即可.
(3)根據(jù)[x]表示不超過x的最大整數(shù),即可解答.
解:(1)①∵第1個數(shù)![]()
第2個數(shù)![]()
第3個數(shù)![]()
…
∴第10個數(shù)為![]() ;
;
由上可知第n個數(shù)為![]() ,
,
∴![]() =
=![]()
∴n(n+1)=306,
解得n=17或n=-18(不合題意,舍去),
∴![]() 是第17個數(shù),
是第17個數(shù),
故答案為:17;
②∵![]() ,
,
∴原式=![]()
![]() .
.
(2)根據(jù)差倒數(shù)定義可得:

可知3個數(shù)為一循環(huán),
∴2019÷3余數(shù)為0,
∴則a2019=a3=4,
故答案為4.
(3)①[-2.1]+[1]=-3+1=-2,故①正確;
②[x]+[-x]=0,錯誤,例如:[2.5]=2,[-2.5]=-3,2+(-3)≠0;
③[2.5]+[-2.5]= 2+(-3)=-1,故③正確;
④當(dāng)x=-0.5時,[x+1]=0,[-x+1]=1,
∴[x+1]+[-x+1]=1,
所以[x+1]+[-x+1]= 2錯誤.
故答案為:①③.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點(diǎn)睛新教材全能解讀系列答案
點(diǎn)睛新教材全能解讀系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀材料: 小明在學(xué)習(xí)二次根式后,發(fā)現(xiàn)一些含根號的式子可以寫成另一個式子的平方,如:![]() ,善于思考的小明進(jìn)行了以下探索:
,善于思考的小明進(jìn)行了以下探索:
設(shè)![]() (其中
(其中![]() 均為整數(shù)),則有
均為整數(shù)),則有![]() .
.
∴![]() .這樣小明就找到了一種把部分
.這樣小明就找到了一種把部分![]() 的式子化為平方式的方法.
的式子化為平方式的方法.
請你仿照小明的方法探索并解決下列問題:
當(dāng)![]() 均為正整數(shù)時,若
均為正整數(shù)時,若![]() ,用含m、n的式子分別表示
,用含m、n的式子分別表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的結(jié)論,找一組正整數(shù)![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均為正整數(shù),求
均為正整數(shù),求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(本題滿分6分)如圖所示的方格地面上,標(biāo)有編號1、2、3的3
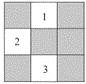
個小方格地面是空地,另外6個小方格地面是草坪,除此以外小方格地
面完全相同.
(1)一只自由飛行的小鳥,將隨意地落在圖中所示的方格地面上,求
小鳥落在草坪上的概率;
(2)現(xiàn)準(zhǔn)備從圖中所示的3個小方格空地中任意選取2個種植草坪,
則編號為1、2的2個小方格空地種植草坪的概率是多少(用樹狀圖或列表法求解)?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
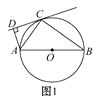
【題目】如圖1,AB是☉O的直徑,C為☉O上一點(diǎn),直線CD與☉O相切于點(diǎn)C,AD⊥CD,垂足為D.
(1)求證:△ACD∽△ABC.
(2)如圖2,將直線CD向下平移與☉O相交于點(diǎn)C,G,但其他條件不變.若AG=4,BG=3,求tan∠CAD的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一個點(diǎn)從數(shù)軸上的原點(diǎn)開始,先向右移動3個單位長度,再向左移動5個單位長度,可以看到終點(diǎn)表示的數(shù)是-2.已知點(diǎn)A,B是數(shù)軸上的點(diǎn),請參照圖并思考,完成下列各題.
![]()
(1) 若點(diǎn)A表示數(shù)![]() ,當(dāng)點(diǎn)A向_____ 移動_____個單位長度時,所表示的數(shù)恰好是4的相反數(shù).
,當(dāng)點(diǎn)A向_____ 移動_____個單位長度時,所表示的數(shù)恰好是4的相反數(shù).
(2) 若點(diǎn)A表示數(shù)![]() ,點(diǎn)B表示數(shù)4,當(dāng)點(diǎn)B不動時,點(diǎn)A向_____移動_____個單位長度或向_____移動_____個單位長度,此時A,B兩點(diǎn)間的距離是6.
,點(diǎn)B表示數(shù)4,當(dāng)點(diǎn)B不動時,點(diǎn)A向_____移動_____個單位長度或向_____移動_____個單位長度,此時A,B兩點(diǎn)間的距離是6.
(3) 若點(diǎn)A表示數(shù)2,將A點(diǎn)向左移動6個單位長度,再向右移動3個單位長度后到達(dá)點(diǎn)B,則B表示的數(shù)是________,此時 A,B兩點(diǎn)間的距離是________.
(4)若A點(diǎn)表示數(shù)為a,將A點(diǎn)向右移動b個單位長度,再向左移動c個單位長度后到達(dá)點(diǎn)B,則點(diǎn)B表示的數(shù)是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,AB=6cm,BC=12cm.∠B=30°.點(diǎn)P在BC上由點(diǎn)B向點(diǎn)C出發(fā),速度為每秒2cm;點(diǎn)Q在邊AD上,同時由點(diǎn)D向點(diǎn)A運(yùn)動,速度為每秒1cm,當(dāng)點(diǎn)P運(yùn)動到點(diǎn)C時,P、Q同時停止運(yùn)動.連接PQ,設(shè)運(yùn)動時間為t秒.
(1)當(dāng)t為何值時四邊形ABPQ為平行四邊形?
(2)設(shè)四邊形ABPQ的面積為y,求y與t之間的函數(shù)關(guān)系式.
(3)當(dāng)t為何值時,四邊形ABPQ的面積是四邊形ABCD的面積的四分之三,并求出此時∠PQD的度數(shù).
(4)連結(jié)AP,是否存在某一時刻t,使△ABP為等腰三角形?并求出此刻t的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】利用如圖1的二維碼可以進(jìn)行身份識別.某校建立了一個身份識別系統(tǒng),圖2是某個學(xué)生的識別圖案,黑色小正方形表示1,白色小正方形表示0.將第一行數(shù)字從左到右依次記為![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以轉(zhuǎn)換為該生所在班級序號,其序號為
,那么可以轉(zhuǎn)換為該生所在班級序號,其序號為![]() .如圖2第一行數(shù)字從左到右依次為0,1,0,1,序號為
.如圖2第一行數(shù)字從左到右依次為0,1,0,1,序號為![]() ,表示該生為5班學(xué)生.表示6班學(xué)生的識別圖案是( )
,表示該生為5班學(xué)生.表示6班學(xué)生的識別圖案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我們知道,一個數(shù)在數(shù)軸上所對應(yīng)的點(diǎn)與原點(diǎn)之間的距離就是這個數(shù)的絕對值。那么任意兩個數(shù)與它們在數(shù)軸上所對應(yīng)的點(diǎn)之間的距離又有什么關(guān)系呢?
(1)如圖所示,-3,-1,2,4在數(shù)軸上分別對應(yīng)點(diǎn)![]() 。
。
![]()
則①點(diǎn)![]() 與原點(diǎn)之間的距離為_______________;②
與原點(diǎn)之間的距離為_______________;②![]() 兩點(diǎn)之間的距離為_____________;
兩點(diǎn)之間的距離為_____________;
③![]() 兩點(diǎn)之間的距離為______________;④
兩點(diǎn)之間的距離為______________;④![]() 兩點(diǎn)之間的距離為_______________。
兩點(diǎn)之間的距離為_______________。
你的結(jié)論:如果兩個數(shù)![]() 在數(shù)軸上分別對應(yīng)點(diǎn)
在數(shù)軸上分別對應(yīng)點(diǎn)![]() ,那么
,那么![]() 與
與![]() 兩點(diǎn)之間的距離表示為______________________。(用含
兩點(diǎn)之間的距離表示為______________________。(用含![]() 的式子表示)
的式子表示)
(2)利用(1)的結(jié)論解決下列問題:
已知數(shù)軸上點(diǎn)![]() 對應(yīng)
對應(yīng)![]() ,點(diǎn)
,點(diǎn)![]() 對應(yīng)3,且
對應(yīng)3,且![]() 與
與![]() 之間的距離是8,求
之間的距離是8,求![]() 的值。
的值。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的中點(diǎn),若點(diǎn)
的中點(diǎn),若點(diǎn)![]() 以
以![]() /秒的速度從點(diǎn)
/秒的速度從點(diǎn)![]() 出發(fā),沿
出發(fā),沿![]() 向點(diǎn)
向點(diǎn)![]() 運(yùn)動:點(diǎn)
運(yùn)動:點(diǎn)![]() 同時以
同時以![]() /秒的速度從點(diǎn)
/秒的速度從點(diǎn)![]() 出發(fā),沿
出發(fā),沿![]() 向點(diǎn)
向點(diǎn)![]() 運(yùn)動,點(diǎn)
運(yùn)動,點(diǎn)![]() 運(yùn)動到
運(yùn)動到![]() 點(diǎn)時停止運(yùn)動,點(diǎn)
點(diǎn)時停止運(yùn)動,點(diǎn)![]() 也時停止運(yùn)動,當(dāng)點(diǎn)
也時停止運(yùn)動,當(dāng)點(diǎn)![]() 運(yùn)動( )秒時,以點(diǎn)
運(yùn)動( )秒時,以點(diǎn)![]() 、
、![]() 、
、、
![]() 為頂點(diǎn)的四邊形是平行四邊形.
為頂點(diǎn)的四邊形是平行四邊形.
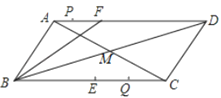
A. 2B. 3C. 3或5D. 4或5
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com