【題目】如圖，在山頂上有一座電視塔，在塔頂B處，測得地面上一點A的俯角α=60°，在塔底C處測得的俯角β=45°，已知BC=60m，求山高CD（精確到1m， 
≈1.732）
【答案】解：設山高CD=x（米），
∵∠CAD=∠β=45°，∠BAD=∠α=60°，∠ADB=90°，
∴AD=CD=x，BD=ADtan60°= 
x．
∵BD﹣CD=BC=60，
∴ x﹣x=60．
∴x= 
=30（ +1）．
∴CD=30×（1.732+1）≈82（米）．
答：山高CD約為82米．
【解析】抓住題中關鍵的已知條件，得出∠CAD和∠BAD的度數，從而可得出AD=CD=x，則根據解直角三角形，可表示出BD的長，再根據BD﹣CD=BC=60，建立關于x的方程，求解即可。
【考點精析】本題主要考查了解一元一次方程的步驟和解直角三角形的相關知識點，需要掌握先去分母再括號，移項變號要記牢．同類各項去合并，系數化“1”還沒好．求得未知須檢驗，回代值等才算了；解直角三角形的依據：①邊的關系a2+b2=c2；②角的關系：A+B=90°；③邊角關系：三角函數的定義．(注意：盡量避免使用中間數據和除法)才能正確解答此題．
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，弦CD⊥AB于點E，點M在⊙O上，MD恰好經過圓心O，連接MB．
（1）若CD=16，BE=4，求⊙O的直徑；
（2）若∠M=∠D，求∠D的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖，若
，將點
在
內部，∠
，∠
，∠滿足的數量關系是 ，并說明理由．
(2)在如圖1中，將直線
繞點逆時針方向旋轉一定角度交直線
于點
，如圖2，利用（1）中的結論（可以直接套用），求∠
﹑∠﹑∠﹑∠
之間有何數量關系？
(3)科技活動課上，雨軒同學制作了一個圖（3）的“飛旋鏢”，經測量發現∠
＝
°，∠
＝
°，則∠
與∠
的數量關系是 .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩家快遞公司攬件員（攬收快件的員工）的日工資方案如下：
甲公司為“基本工資+攬件提成”，其中基本工資為70元/日，每攬收一件提成2元；
乙公司無基本工資，僅以攬件提成計算工資．若當日攬件數不超過40，每件提成4元；若當日攪件數超過40，超過部分每件多提成2元．
如圖是今年四月份甲公司攬件員人均攬件數和乙公司攪件員人均攬件數的條形統計圖：
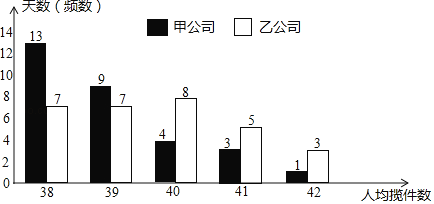
（1）現從今年四月份的30天中隨機抽取1天，求這一天甲公司攬件員人均攬件數超過40（不含40）的概率；
（2）根據以上信息，以今年四月份的數據為依據，并將各公司攬件員的人均攬件數視為該公司各攬件員的
攬件數，解決以下問題：
①估計甲公司各攬件員的日平均件數；
②小明擬到甲、乙兩家公司中的一家應聘攬件員，如果僅從工資收入的角度考慮，請利用所學的統計知識幫他選擇，井說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】由于霧霾天氣持續籠罩某地區，口罩市場出現熱賣.某商店用8000元購進甲、乙兩種口罩，銷售完后共獲利2800元，其進價和售價如下表：
甲種口罩 | 乙種口罩 | |
進價（元/袋） | 20 | 25 |
售價（元/袋） | 26 | 35 |
（1）求該商店購進甲、乙兩種口罩各多少袋？
（2）該商店第二次仍以原價購進甲、乙兩種口罩，購進乙種口罩袋數不變，而購進甲種口罩袋數是第一次的2倍，甲種口罩按原售價出售，而乙種口罩讓利銷售.若兩種口罩銷售完畢，要使第二次銷售活動獲利不少于3680元，則乙種口罩最低售價為每袋多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點A、B在反比例函數 
的圖象上，且點A、B的橫坐標分別為a、2a（a＞0），AC⊥x軸，垂足為C，且△AOC的面積為2，
（1）求該反比例函數的解析式；
（2）求△AOB的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（背景介紹）勾股定理是幾何學中的明珠，充滿著魅力．千百年來，人們對它的證明趨之若騖，其中有著名的數學家，也有業余數學愛好者．向常春在1994年構造發現了一個新的證法．
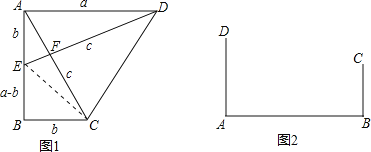
（小試牛刀）把兩個全等的直角三角形如圖1放置，其三邊長分別為a、b、c．顯然，∠DAB=∠B=90°，AC⊥DE．請用a、b、c分別表示出梯形ABCD、四邊形AECD、△EBC的面積，再探究這三個圖形面積之間的關系，可得到勾股定理：
S梯形ABCD= ，
S△EBC= ，
S四邊形AECD= ，
則它們滿足的關系式為 ，經化簡，可得到勾股定理．
（知識運用）（1）如圖2，鐵路上A、B兩點（看作直線上的兩點）相距40千米，C、D為兩個村莊（看作兩個點），AD⊥AB，BC⊥AB，垂足分別為A、B，AD=25千米，BC=16千米，則兩個村莊的距離為 千米（直接填空）；
（2）在（1）的背景下，若AB=40千米，AD=24千米，BC=16千米，要在AB上建造一個供應站P，使得PC=PD，請用尺規作圖在圖2中作出P點的位置并求出AP的距離．
（知識遷移）借助上面的思考過程與幾何模型，求代數式
最小值（0＜x＜16）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
