
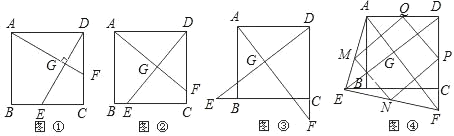
【題目】如圖1,在正方形ABCD中,點E、F分別為邊BC、CD的中點,AF、DE相交于點G,則可得結論:①AF=DE,②AF⊥DE(不須證明).
(1)如圖②,若點E、F不是正方形ABCD的邊BC、CD的中點,但滿足CE=DF,則上面的結論①、②是否仍然成立;(請直接回答“成立”或“不成立”)
(2)如圖③,若點E、F分別在正方形ABCD的邊CB的延長線和DC的延長線上,且CE=DF,此時上面的結論①、②是否仍然成立?若成立,請寫出證明過程;若不成立,請說明理由.
(3)如圖④,在(2)的基礎上,連接AE和EF,若點M、N、P、Q分別為AE、EF、FD、AD的中點,請先判斷四邊形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一種,并寫出證明過程.
 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案科目:初中數學 來源: 題型:
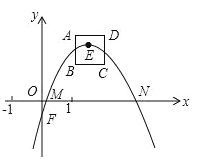
【題目】如圖,拋物線l:y=﹣x2+bx+c(b,c為常數),其頂點E在正方形ABCD內或邊上,已知點A(1,2),B(1,1),C(2,1).
(1)直接寫出點D的坐標_____________;
(2)若l經過點B,C,求l的解析式;
(3)設l與x軸交于點M,N,當l的頂點E與點D重合時,求線段MN的值;當頂點E在正方形ABCD內或邊上時,直接寫出線段MN的取值范圍;
(4)若l經過正方形ABCD的兩個頂點,直接寫出所有符合條件的c的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,拋物線y=x2+bx+c過點A(3,0),B(1,0),交y軸于點C,點P是該拋物線上一動點,點P從C點沿拋物線向A點運動(點P不與點A重合),過點P作PD∥y軸交直線AC于點D.
(1)求拋物線的解析式;
(2)求點P在運動的過程中線段PD長度的最大值;
(3)△APD能否構成直角三角形?若能請直接寫出點P坐標,若不能請說明理由;
(4)在拋物線對稱軸上是否存在點M使|MA﹣MC|最大?若存在請求出點M的坐標,若不存在請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下面的點陣圖和相應的等式,探究其中的規律:
(1)認真觀察,并在④后面的橫線上寫出相應的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)結合(1)觀察下列點陣圖,并在⑤后面的橫線上寫出相應的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通過猜想,寫出(2)中與第n個點陣相對應的等式 .
【答案】(1)10;(2)見解析;(3)![]()
【解析】試題分析:(1)根據①②③觀察會發現第四個式子的等號的左邊是1+2+3+4,右邊分子上是(1+4)×4,從而得到規律;
(2)通過觀察發現左邊是10+15,右邊是25即5的平方;
(3)過對一些特殊式子進行整理、變形、觀察、比較,歸納出一般規律.
試題解析:(1)根據題中所給出的規律可知:1+2+3+4=![]() =10;
=10;
(2)由圖示可知點的總數是5×5=25,所以10+15=52.
(3)由(1)(2)可知![]()
點睛:主要考查了學生通過特例分析從而歸納總結出一般結論的能力.對于找規律的題目首先應找出哪些部分發生了變化,是按照什么規律變化的.通過分析找到各部分的變化規律后用一個統一的式子表示出變化規律是此類題目中的難點.
【題型】解答題
【結束】
19
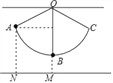
【題目】如圖,用細線懸掛一個小球,小球在豎直平面內的A、C兩點間來回擺動,A點與地面距離AN=14cm,小球在最低點B時,與地面距離BM=5cm,∠AOB=66°,求細線OB的長度.(參考數據:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某研究性學習小組進行了探究活動.如圖,已知一架竹梯AB斜靠在墻角MON處,竹梯AB=13m,梯子底端離墻角的距離BO=5m.
(1)求這個梯子頂端A距地面有多高;
(2)如果梯子的頂端A下滑4 m到點C,那么梯子的底部B在水平方向上滑動的距離BD=4 m嗎?為什么?
(3)亮亮在活動中發現無論梯子怎么滑動,在滑動的過程中梯子上總有一個定點到墻角O的距離始終是不變的定值,會思考問題的你能說出這個點并說明其中的道理嗎?

查看答案和解析>>
科目:初中數學 來源: 題型:
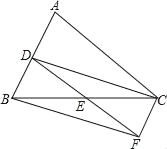
【題目】已知:如圖,在△ABC中,D、E分別是AB、BC邊上的中點,過點C作CF∥AB,交DE的延長線于F點,連接CD、BF.
(1)求證:△BDE≌△CFE;
(2)△ABC滿足什么條件時,四邊形BDCF是矩形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“愛我中華”中學生演講比賽中,五位評委分別給甲、乙兩位選手的評分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,則下列說法中錯誤的是( )
A. 甲得分的方差比乙得分的方差小B. 甲得分的眾數是8,乙得分的眾數是9
C. 甲、乙得分的平均數都是8D. 甲得分的中位數是9,乙得分的中位數是6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛最大載重48噸的大型貨車,貨車的貨箱是長14m,寬2.5m,高3m的長方體,現有甲種貨物18噸,乙種貨物70m3,而甲種貨物每噸的體積為2.5m3,乙種貨物每立方米0.5噸.問:
(1)甲、乙兩種貨物是否都能裝上車?請說明理由.
(2)為了最大地利用車的載重量和貨箱的容積,兩種貨物應各裝多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠ABC=90°,D是直線AB上的點,AD=BC.
(1)如圖1,過點A作AF⊥AB,截取AF=BD,連接DC、DF、CF,判斷△CDF的形狀并證明;
(2)如圖2,E是直線BC上一點,且CE=BD,直線AE、CD相交于點P,∠APD的度數是一個固定的值嗎?若是,請求出它的度數;若不是,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com