
科目: 來源: 題型:
【題目】某學校運動會的立定跳遠和30秒跳繩兩個單項比賽分成預賽和決賽兩個階段,下表為10名學生的預賽成績,其中有三個數據模糊.
學生序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
跳遠(米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
跳繩(次) | 63 |
| 75 | 60 | 63 | 72 | 70 |
|
| 65 |
在這10名學生中,進入立定跳遠決賽的有8人,同時進入立定跳遠決賽和30秒跳繩決賽的有6人,則( )
A.5號學生進入30秒跳繩決賽
B.2號學生進入30秒跳繩決賽
C.8號學生進入30秒跳繩決賽
D.9號學生進入30秒跳繩決賽
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,是根據某市2010年至2014年工業生產總值繪制的折線統計圖,觀察統計圖獲得以下信息,其中信息判斷錯誤的是( )

A.2010年至2014年間工業生產總值逐年增加
B.2014年的工業生產總值比前一年增加了40億元
C.2012年與2013年每一年與前一年比,其增長額相同
D.從2011年至2014年,每一年與前一年比,2014年的增長率最大
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,已知一次函數![]() 的圖象經過
的圖象經過![]() ,與y軸交于點C,拋物線
,與y軸交于點C,拋物線![]() 與x軸交于點A,B(點A在點B的左側),交直線
與x軸交于點A,B(點A在點B的左側),交直線![]() 于點P.
于點P.
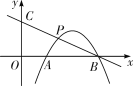
(1)若![]() ,求拋物線的解析式;
,求拋物線的解析式;
(2)若點P是線段![]() 的中點,求a的值;
的中點,求a的值;
(3)設點P的橫坐標為![]() ,則當
,則當![]() 時,直接寫出此時a的取值范圍.
時,直接寫出此時a的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,一次函數![]() 的圖象
的圖象![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() :
:![]() 與
與![]() 軸的交點分別為
軸的交點分別為![]() 、
、![]() (點
(點![]() 在點
在點![]() 的左側).
的左側).

(1)當![]() 的頂點在
的頂點在![]() 上時,求
上時,求![]() 的值;
的值;
(2)若![]() 、
、![]() 兩點中有一點與點
兩點中有一點與點![]() 關于原點對稱,試判斷這個點是點
關于原點對稱,試判斷這個點是點![]() 還是點
還是點![]() ;
;
(3)若![]() 的頂點為
的頂點為![]() ,對稱軸與
,對稱軸與![]() 的交點為
的交點為![]() ,且點
,且點![]() 在點
在點![]() 的下方,當
的下方,當![]() 為何值時,線段
為何值時,線段![]() 的長最大.
的長最大.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,拋物線![]() :
:![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,直線
兩點,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 的對稱軸交于點
的對稱軸交于點![]() ,與
,與![]() 交于點
交于點![]() ,拋物線
,拋物線![]() 的對稱軸與
的對稱軸與![]() 交于點
交于點![]() .
.
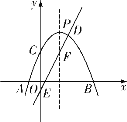
(1)求![]() 的值;
的值;
(2)點![]() 能否與點
能否與點![]() 關于
關于![]() 軸的對稱點重合?若認為能,請求出
軸的對稱點重合?若認為能,請求出![]() 的值;若認為不能,說明理由;
的值;若認為不能,說明理由;
(3)小林研究了拋物線![]() 的解析式后,得到了如下的結論:因為
的解析式后,得到了如下的結論:因為![]() 可以取任意實數,所以點
可以取任意實數,所以點![]() 可以在
可以在![]() 軸上任意移動,即
軸上任意移動,即![]() 點可以到達
點可以到達![]() 軸的任何位置,你認為他說的有道理嗎?說說你的理由;
軸的任何位置,你認為他說的有道理嗎?說說你的理由;
(4)當拋物線![]() 與直線
與直線![]() 有兩個公共點時,直接寫出適合條件的
有兩個公共點時,直接寫出適合條件的![]() 的最大整數.
的最大整數.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A(5,3),點B(﹣3,3),過點A的直線y=![]() x+m(m為常數)與直線x=1交于點P,與x軸交于點C,直線BP與x軸交于點D.
x+m(m為常數)與直線x=1交于點P,與x軸交于點C,直線BP與x軸交于點D.
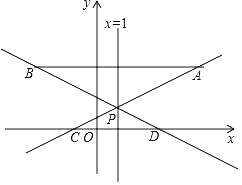
(1)求點P的坐標;
(2)求直線BP的解析式,并直接寫出△PCD與△PAB的面積比;
(3)若反比例函數![]() (k為常數且k≠0)的圖象與線段BD有公共點時,請直接寫出k的最大值或最小值.
(k為常數且k≠0)的圖象與線段BD有公共點時,請直接寫出k的最大值或最小值.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知,在平面直角坐標系![]() 中,拋物線
中,拋物線![]() :
:![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),頂點為
的左側),頂點為![]() .
.
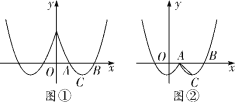
(1)求點![]() 和點
和點![]() 的坐標;
的坐標;
(2)定義“![]() 雙拋圖形”:直線
雙拋圖形”:直線![]() 將拋物線
將拋物線![]() 分成兩部分,首先去掉其不含頂點的部分,然后作出拋物線剩余部分關于直線
分成兩部分,首先去掉其不含頂點的部分,然后作出拋物線剩余部分關于直線![]() 的對稱圖形,得到的整個圖形稱為拋物線
的對稱圖形,得到的整個圖形稱為拋物線![]() 關于直線
關于直線![]() 的“
的“![]() 雙拋圖形”(特別地,當直線
雙拋圖形”(特別地,當直線![]() 恰好是拋物線的對稱軸時,得到的“
恰好是拋物線的對稱軸時,得到的“![]() 雙拋圖形”不變).
雙拋圖形”不變).
①當![]() 時,拋物線
時,拋物線![]() 關于直線
關于直線![]() 的“
的“![]() 雙拋圖形”如圖①所示,直線
雙拋圖形”如圖①所示,直線![]() 與“
與“![]() 雙拋圖形”有________個交點;
雙拋圖形”有________個交點;
②若拋物線![]() 關于直線
關于直線![]() 的“
的“![]() 雙拋圖形”與直線
雙拋圖形”與直線![]() 恰好有兩個交點,結合圖象,直接寫出
恰好有兩個交點,結合圖象,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,在直角坐標系中,點![]() 的坐標是
的坐標是![]() ,拋物線
,拋物線![]() 經過原點
經過原點![]() 和點
和點![]() ,已知正方形
,已知正方形![]() 的三個頂點為
的三個頂點為![]() ,
,![]() ,
,![]() .
.
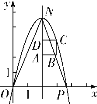
(1)若當![]() 時,求
時,求![]() ,
,![]() ,并寫出拋物線對稱軸及
,并寫出拋物線對稱軸及![]() 的最大值;
的最大值;
(2)求證:拋物線的頂點在函數![]() 的圖象上;
的圖象上;
(3)若拋物線與直線![]() 交于點
交于點![]() ,求
,求![]() 為何值時,
為何值時,![]() 的面積為1;
的面積為1;
(4)若拋物線經過正方形區域![]() (含邊界),請直接寫出
(含邊界),請直接寫出![]() 的取值范圍.
的取值范圍.
(參考公式:![]() 的頂點坐標是
的頂點坐標是 .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知拋物線y=ax2﹣ax﹣2a(a為常數且不等于0)與x軸的交點為A,B兩點,且A點在B的右側.
(1)當拋物線經過點(3,8),求a的值;
(2)求A、B兩點的坐標;
(3)若拋物線的頂點為M,且點M到x軸的距離等于AB的3倍,求拋物線的解析式.
查看答案和解析>>
科目: 來源: 題型:
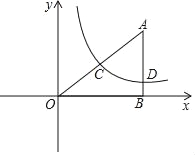
【題目】如圖,Rt△ABO在直角坐標系中,AB⊥x軸于點B,AO=10,sin∠AOB=![]() .
.
(1)若反比例函數y=![]() (x>0)的圖象經過AO的中點C,求k的值;
(x>0)的圖象經過AO的中點C,求k的值;
(2)在(1)的條件下,若反比例函數y=![]() (x>0)的圖象與AB交于點D,當點C,D位于直線l:y=﹣x+b的異側時,求b的取值范圍;
(x>0)的圖象與AB交于點D,當點C,D位于直線l:y=﹣x+b的異側時,求b的取值范圍;
(3)若點D關于y軸的對稱點為E,當反比例函數y=![]() 的圖象和線段AE有公共點時,直接寫出k的取值范圍.
的圖象和線段AE有公共點時,直接寫出k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com