
【題目】已知函數f(x)=sinπx,g(x)=x2﹣x+2,則( )
A. 曲線y=f(x)+g(x)不是軸對稱圖形
B. 曲線y=f(x)﹣g(x)是中心對稱圖形
C. 函數y=f(x)g(x)是周期函數
D. 函數![]() 最大值為
最大值為![]()
【答案】D
【解析】
根據題意,依次分析選項,綜合即可得答案.
根據題意,依次分析選項:
對于A,函數f(x)=sinπx,為軸對稱圖形,且其中一條對稱軸為x![]() ,
,
g(x)=x2﹣x+2=(x![]() )2
)2![]() ,為軸對稱圖形,且其對稱軸為x
,為軸對稱圖形,且其對稱軸為x![]() ,
,
故y=f(x)+g(x)=sinπx+(x2﹣x+2)是軸對稱圖形,且其對稱軸為x![]() ,A錯誤;
,A錯誤;
對于B,g(x)=x2﹣x+2,不是中心對稱圖形,則曲線y=f(x)﹣g(x)不是中心對稱圖形,B錯誤;
對于C,g(x)=x2﹣x+2不是周期函數,f(x)g(x)=(sinπx)(x2﹣x+2)不是周期函數,C錯誤;
對于D,g(x)=x2﹣x+2=(x![]() )2
)2![]() ,當x
,當x![]() 時,g(x)取得最小值
時,g(x)取得最小值![]() ,
,
而f(x)=sinπx,當x![]() 時,f(x)取得最大值1,
時,f(x)取得最大值1,
則函數![]() 最大值為
最大值為![]() ;D正確;
;D正確;
故選:D.


科目:高中數學 來源: 題型:
【題目】已知拋物線E:x2=2py(p>0)的焦點為F,點M是直線y=x與拋物線E在第一象限內的交點,且|MF|=5.
(1)求拋物E的方程.
(2)直線l與拋物線E相交于兩點A,B,過點A,B分別作AA1⊥x軸于A1,BB1⊥x軸于B1,原點O到直線l的距離為1.求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 1(a>b>0)經過點(
1(a>b>0)經過點(![]() ,1),F(0,1)是C的一個焦點,過F點的動直線l交橢圓于A,B兩點.
,1),F(0,1)是C的一個焦點,過F點的動直線l交橢圓于A,B兩點.
(1)求橢圓C的方程
(2)是否存在定點M(異于點F),對任意的動直線l都有kMA+kMB=0,若存在求出點M的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,其短軸的兩個端點與長軸的一個端點構成的三角形的面積為
,其短軸的兩個端點與長軸的一個端點構成的三角形的面積為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 與圓
與圓![]() 相切,并與橢圓
相切,并與橢圓![]() 交于不同的兩點
交于不同的兩點![]() 和
和![]() ,若
,若![]() 為坐標原點),求線段
為坐標原點),求線段![]() 長度的取值范圍.
長度的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個關于圓錐曲線的命題中
①設A.B為兩個定點,k為非零常數,![]() ,則動點P的軌跡為雙曲線;
,則動點P的軌跡為雙曲線;
②曲線![]() 表示焦點在y軸上的橢圓,則
表示焦點在y軸上的橢圓,則![]() ;
;
③方程![]() 的兩根可分別作為橢圓和雙曲線的離心率;
的兩根可分別作為橢圓和雙曲線的離心率;
④雙曲![]() 與橢圓
與橢圓![]() 有相同的焦點.
有相同的焦點.
其中真命題的序號( )
A.②③④B.①②③C.①③④D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汕頭某家電企業要將剛剛生產的100臺變頻空調送往市內某商場,現有4輛甲型貨車和8輛乙型貨車可供調配,每輛甲型貨車的運輸費用是400元,可裝空調20臺,每輛乙型貨車的運輸費用是300元,可裝空調10臺,若每輛車至多運一次,則企業所花的最少運費為( )
A. 2000元B. 2200元C. 2400元D. 2800元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:實數x滿足x2﹣4ax+3a2<0(a>0),命題q:實數x滿足x2﹣5x+6<0.
(1)若a=1,且p∧q為真命題,求實數x的取值范圍;
(2)若p是q的必要不充分條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩位同學分別做下面這道題目:在平面直角坐標系中,動點![]() 到
到![]() 的距離比
的距離比![]() 到
到![]() 軸的距離大
軸的距離大![]() ,求
,求![]() 的軌跡.甲同學的解法是:解:設
的軌跡.甲同學的解法是:解:設![]() 的坐標是
的坐標是![]() ,則根據題意可知
,則根據題意可知
![]() ,化簡得
,化簡得![]() ; ①當
; ①當![]() 時,方程可變為
時,方程可變為![]() ;②這表示的是端點在原點、方向為
;②這表示的是端點在原點、方向為![]() 軸正方向的射線,且不包括原點; ③當
軸正方向的射線,且不包括原點; ③當![]() 時,方程可變為
時,方程可變為![]() ; ④這表示以
; ④這表示以![]() 為焦點,以直線
為焦點,以直線![]() 為準線的拋物線;⑤所以
為準線的拋物線;⑤所以![]() 的軌跡為端點在原點、方向為
的軌跡為端點在原點、方向為![]() 軸正方向的射線,且不包括原點和以
軸正方向的射線,且不包括原點和以![]() 為焦點,以直線
為焦點,以直線![]() 為準線的拋物線. 乙同學的解法是:解:因為動點
為準線的拋物線. 乙同學的解法是:解:因為動點![]() 到
到![]() 的距離比
的距離比![]() 到
到![]() 軸的距離大
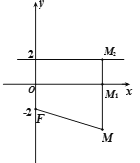
軸的距離大![]() . ①如圖,過點
. ①如圖,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() . 則
. 則![]() .設直線
.設直線![]() 與直線
與直線![]() 的交點為
的交點為![]() ,則
,則![]() ; ②即動點
; ②即動點![]() 到直線
到直線![]() 的距離比
的距離比![]() 到
到![]() 軸的距離大
軸的距離大![]() ; ③所以動點
; ③所以動點![]() 到
到![]() 的距離與
的距離與![]() 到直線
到直線![]() 的距離相等;④所以動點
的距離相等;④所以動點![]() 的軌跡是以
的軌跡是以![]() 為焦點,以直線
為焦點,以直線![]() 為準線的拋物線; ⑤甲、乙兩位同學中解答錯誤的是________(填“甲”或者“乙”),他的解答過程是從_____處開始出錯的(請在橫線上填寫① 、②、③、④ 或⑤ ).
為準線的拋物線; ⑤甲、乙兩位同學中解答錯誤的是________(填“甲”或者“乙”),他的解答過程是從_____處開始出錯的(請在橫線上填寫① 、②、③、④ 或⑤ ).
查看答案和解析>>
科目:高中數學 來源: 題型:
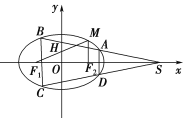
【題目】如圖,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() 軸,直線
軸,直線![]() 交
交![]() 軸于
軸于![]() 點,
點,![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 的面積的最大值為1.
的面積的最大值為1.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作兩條直線與橢圓
作兩條直線與橢圓![]() 分別交于
分別交于![]() 且使
且使![]() 軸,如圖,問四邊形
軸,如圖,問四邊形![]() 的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com