
【題目】如圖,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() .過
.過![]() 的平面交
的平面交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.
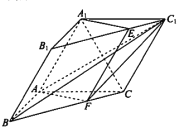
(l)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求證: ![]() ;
;
(Ⅲ)記四棱錐![]() 的體積為
的體積為![]() ,三棱柱
,三棱柱![]() 的體積為
的體積為![]() .若
.若![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)證明見解析;(Ⅱ)證明見解析;(Ⅲ) ![]() .
.
【解析】試題分析:(l)因為![]() 平面
平面![]() ,由線面垂直的性質可得
,由線面垂直的性質可得![]() ,根據菱形的性質可得
,根據菱形的性質可得![]() ,利用線面垂直的判定定理可得
,利用線面垂直的判定定理可得![]() 平面
平面![]() ;(Ⅱ)由
;(Ⅱ)由![]() ,
, ![]() 平面
平面![]() ,所以
,所以 ![]() 平面
平面![]() ,利用線面平行的性質定理可得
,利用線面平行的性質定理可得![]() ;(Ⅲ) 記三棱錐
;(Ⅲ) 記三棱錐![]() 的體積為
的體積為![]() ,三棱柱
,三棱柱![]() 的體積為
的體積為![]() ,先證明
,先證明![]() ,所以
,所以 ![]() ,結合
,結合![]() , 可得
, 可得 ![]() ,而三棱柱
,而三棱柱![]() 與三棱柱
與三棱柱![]() 等高,由此得
等高,由此得 ![]() .
.
試題解析:(1) 因為 ![]() 平面
平面![]() ,所以
,所以 ![]() .
.
在三棱柱![]() 中,因為
中,因為 ![]() ,所以 四邊形
,所以 四邊形![]() 為菱形,
為菱形,
所以 ![]() . 所以
. 所以 ![]() 平面
平面![]() .
.
(2)在 三棱柱![]() 中,
中,
因為 ![]() ,
, ![]() 平面
平面![]() ,所以
,所以 ![]() 平面
平面![]() .
.
因為 平面![]() 平面
平面![]() ,所以
,所以 ![]() .
.
(3)記三棱錐![]() 的體積為
的體積為![]() ,三棱柱
,三棱柱![]() 的體積為
的體積為![]() .
.
因為三棱錐![]() 與三棱柱
與三棱柱![]() 同底等高,
同底等高,
所以 ![]() , 所以
, 所以 ![]() .
.
因為 ![]() , 所以
, 所以 ![]() . 因為 三棱柱
. 因為 三棱柱![]() 與三棱柱
與三棱柱![]() 等高,
等高,
所以 △![]() 與△
與△![]() 的面積之比為
的面積之比為![]() , 所以
, 所以 ![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖所示,已知兩個正方形ABCD和DCEF不在同一平面內,M,N分別為AB,DF的中點.
(1)若平面ABCD⊥平面DCEF,求直線MN與平面DCEF所成角的正弦值;
(2)用反證法證明:直線ME與BN是兩條異面直線.
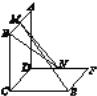
查看答案和解析>>
科目:高中數學 來源: 題型:
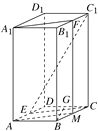
【題目】(2017·泰安模擬)如圖,在正四棱柱ABCDA1B1C1D1中,E為AD的中點,F為B1C1的中點.
(1)求證:A1F∥平面ECC1;
(2)在CD上是否存在一點G,使BG⊥平面ECC1?若存在,請確定點G的位置,并證明你的結論,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著“中華好詩詞”節目的播出,掀起了全民誦讀傳統詩詞經典的熱潮.某大學社團為調查大學生對于“中華詩詞”的喜好,在該校隨機抽取了40名學生,記錄他們每天學習“中華詩詞”的時間,并整理得到如下頻率分布直方圖:
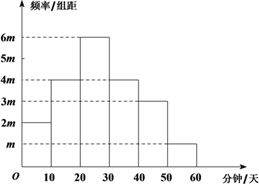
根據學生每天學習“中華詩詞”的時間,可以將學生對于“中華詩詞”的喜好程度分為三個等級 :
學習時間 (分鐘/天) |
|
|
|
等級 | 一般 | 愛好 | 癡迷 |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 從該大學的學生中隨機選出一人,試估計其“愛好”中華詩詞的概率;
(Ⅲ) 假設同組中的每個數據用該組區間的右端點值代替,試估計樣本中40名學生每人每天學習“中華詩詞”的時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市高中全體學生參加某項測評,按得分評為![]() 兩類(評定標準見表1).根據男女學生比例,使用分層抽樣的方法隨機抽取了10000名學生的得分數據,其中等級為
兩類(評定標準見表1).根據男女學生比例,使用分層抽樣的方法隨機抽取了10000名學生的得分數據,其中等級為![]() 的學生中有40%是男生,等級為
的學生中有40%是男生,等級為![]() 的學生中有一半是女生.等級為
的學生中有一半是女生.等級為![]() 和
和![]() 的學生統稱為
的學生統稱為![]() 類學生,等級為
類學生,等級為![]() 和
和![]() 的學生統稱為
的學生統稱為![]() 類學生.整理這10000名學生的得分數據,得到如圖2所示的頻率分布直方圖,
類學生.整理這10000名學生的得分數據,得到如圖2所示的頻率分布直方圖,
類別 | 得分( | |
|
|
|
|
| |
|
|
|
|
| |
表1
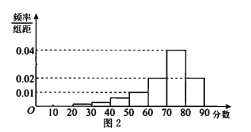
(I)已知該市高中學生共20萬人,試估計在該項測評中被評為![]() 類學生的人數;
類學生的人數;
(Ⅱ)某5人得分分別為45,50,55,75,85.從這5人中隨機選取2人組成甲組,另外3人組成乙組,求“甲、乙兩組各有1名![]() 類學生”的概率;
類學生”的概率;
(Ⅲ)在這10000名學生中,男生占總數的比例為51%, ![]() 類女生占女生總數的比例為
類女生占女生總數的比例為![]() ,
, ![]() 類男生占男生總數的比例為
類男生占男生總數的比例為![]() ,判斷
,判斷![]() 與
與![]() 的大小.(只需寫出結論)
的大小.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() ,以平面直角坐標系
,以平面直角坐標系![]() 的原點
的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線
軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線![]() .
.
(1)將曲線![]() 上的所有點的橫坐標、縱坐標分別伸長為原來的
上的所有點的橫坐標、縱坐標分別伸長為原來的![]() 倍、2倍后得到曲線
倍、2倍后得到曲線![]() .試寫出直線
.試寫出直線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的參數方程;
的參數方程;
(2)在曲線![]() 上求一點
上求一點![]() ,使點
,使點![]() 到直線
到直線![]() 的距離最大,并求出此最大值.
的距離最大,并求出此最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,圓![]() 的極坐標方程為:
的極坐標方程為: ![]() .若以極點
.若以極點![]() 為原點,極軸所在直線為
為原點,極軸所在直線為![]() 軸建立平面直角坐標系.
軸建立平面直角坐標系.
(Ⅰ)求圓![]() 的參數方程;
的參數方程;
(Ⅱ)在直角坐標系中,點![]() 是圓
是圓![]() 上動點,試求
上動點,試求![]() 的最大值,并求出此時點
的最大值,并求出此時點![]() 的直角坐標.
的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為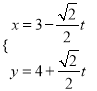 (
(![]() 為參數),在以原點
為參數),在以原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸的極坐標系中,圓
軸正半軸為極軸的極坐標系中,圓![]() 的方程為
的方程為![]() .
.
(1)寫出直線![]() 的普通方程和圓
的普通方程和圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() ,直線
,直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com