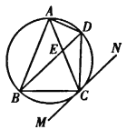
【題目】如圖，
內接于
，
，直線
切于點
，弦
，
與
交于點
.
(1)求證：
；
(2)若
，
，求
.
【答案】
【解析】
22．（本小題滿分10分）選修4－1：幾何證明選講
解:（Ⅰ）在ΔABE和ΔACD中，
∵
∠ABE=∠ACD………………2分
又，∠BAE=∠EDC
∵BD//MN
∴∠EDC=∠DCN
∵直線是圓的切線，
∴∠DCN=∠CAD
∴∠BAE=∠CAD
∴Δ
Δ
（角、邊、角）……………………………5分
（Ⅱ）
∵∠EBC=∠BCM ∠BCM=∠BDC
∴∠EBC=∠BDC=∠BAC BC=CD=4
又 ∠BEC=∠BAC+∠ABE=∠EBC+∠ABE=∠ABC=∠ACB
∴ BC="BE=4 " ……………………………8分
設AE=
，易證 ΔABE∽ΔDEC
∴
又
∴……………………………10分
科目：高中數學 來源： 題型：
【題目】2019年，隨著中國第一款5G手機投入市場，5G技術已經進入高速發展階段.已知某5G手機生產廠家通過數據分析，得到如下規律：每生產手機
萬臺，其總成本為
，其中固定成本為800萬元，并且每生產1萬臺的生產成本為1000萬元（總成本=固定成本+生產成本），銷售收入
萬元滿足
（1）將利潤
表示為產量
萬臺的函數；
（2）當產量為何值時，公司所獲利潤最大？最大利潤為多少萬元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=4cosxsin（x+
）-1．
（1）求f（x）的最小正周期和單調遞減區間；
（2）將y=f（x）圖象上所有的點向右平行移動個單位長度，得到y=g（x）的圖象．若g（x）在（0，m）內是單調函數，求實數m的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個工廠生產某種產品每年需要固定投資100萬元,此外每生產1件該產品還需要增加投資1萬元,年產量為
（
）件.當
時，年銷售總收人為（
）萬元；當
時，年銷售總收人為
萬元.記該工廠生產并銷售這種產品所得的年利潤為
萬元.(年利潤=年銷售總收入一年總投資)
(1)求(萬元)與(件)的函數關系式；
(2)當該工廠的年產量為多少件時,所得年利潤最大?最大年利潤是多少?
查看答案和解析>>
科目：高中數學 來源： 題型：
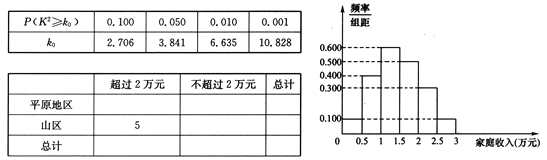
【題目】某貧困地區有1500戶居民，其中平原地區1050戶，山區450戶.為調查該地區2017年家庭收入情況，從而更好地實施“精準扶貧”，采用分層抽樣的方法，收集了150戶家庭2017年年收入的樣本數據（單位：萬元）.
（Ⅰ）應收集多少戶山區家庭的樣本數據？
（Ⅱ）根據這150個樣本數據，得到2017年家庭收入的頻率分布直方圖（如圖所示），其中樣本數據分組區間為
，
，
，，
，
，
.如果將頻率視為概率，估計該地區2017年家庭收入超過1.5萬元的概率；
（Ⅲ）樣本數據中，由5戶山區家庭的年收入超過2萬元，請完成2017年家庭收入與地區的列聯表，并判斷是否有
的把握認為“該地區2017年家庭年收入與地區有關”？
附：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標平面上，稱橫、縱坐標都是有理數的點為有理點．求滿足如下條件的最小正整數
：每一個圓周上含有個有理點的圓，它的圓周上一定含有無窮多個有理點．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的半焦距為
，圓
與橢圓
有且僅有兩個公共點，直線
與橢圓只有一個公共點.
（1）求橢圓的標準方程；
（2）已知動直線
過橢圓的左焦點
，且與橢圓分別交于
兩點，試問：
軸上是否存在定點
，使得
為定值?若存在，求出該定值和點的坐標；若不存在，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
