Question

【題目】已知橢圓的左、右焦點分別為F1，F2，過點F1的直線與C交于A，B兩點.△ABF2的周長為，且橢圓的離心率為.

（1）求橢圓C的標準方程：

（2）設點P為橢圓C的下頂點，直線PA，PB與y＝2分別交于點M，N，當|MN|最小時，求直線AB的方程.

Answer 1

【答案】（1）（2）x﹣y+1＝0

【解析】

（1）根據三角形的周長求得，結合橢圓離心率和求得的值，由此求得橢圓的標準方程.

（2）設出直線的方程，聯立直線的方程和橢圓的方程，寫出韋達定理.通過直線的方程求得，通過直線的方程求得，由此求得的表達式并進行化簡，對進行分類討論，由此求得的最小值以及此時直線的方程.

（1）由題意可得：4a＝，，

∴a，c＝1，∴b2＝a2﹣c2＝1，

∴橢圓C的方程為：；

（2）點P（0，﹣1），F1（﹣1，0），設A（x1，y1），B（x2，y2），

顯然直線AB與x軸不重合，設直線AB的方程為：x＝my﹣1，則可知m≠﹣1，

聯立方程，消去y得：（m2+2）y2﹣2my﹣1＝0，

∴，，

直線PA的方程為：（y1+1）x﹣x1y﹣x1＝0，可得，

同理，

|MN|＝||＝3||＝3，

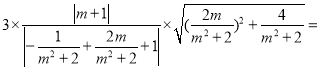
當m＝0時，|MN|＝6，

當m≠0時，|MN|＝，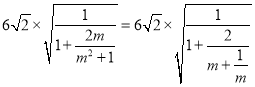

由于m∈（﹣∞，﹣2）∪[2，+∞），則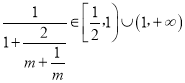，此時|MN|的最小值為6＜，在m＝1處取得，

綜上所述，當|MN|最小時，直線AB的方程為：x＝y﹣1，即x﹣y+1＝0.