
【題目】設函數![]() .
.
(1)當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(2)若對任意![]() 及任意
及任意![]() ,
, ![]() ,恒有
,恒有![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)詳見解析;(2)![]() .
.
【解析】試題分析:
(1)由函數的導函數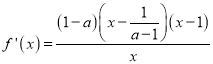 分類討論可得:
分類討論可得:
當![]() 時,
時, ![]() 在定義域上是減函數;
在定義域上是減函數;
當![]() 時,
時, ![]() 在
在![]() ,
, ![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時, ![]() 在
在![]() 和
和![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
(2)結合(1)的結論可得![]() ,構造函數
,構造函數![]() ,討論可得
,討論可得![]() .
.
試題解析:(1)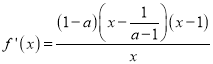 ,
,
當![]() ,即
,即![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上是減函數;
上是減函數;
當![]() ,即
,即![]() 時,令
時,令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ;
;
當![]() ,即
,即![]() 時,令
時,令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ;
;
綜上,當![]() 時,
時, ![]() 在定義域上是減函數;
在定義域上是減函數;
當![]() 時,
時, ![]() 在
在![]() ,
, ![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時, ![]() 在
在![]() 和
和![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
(2)由(1)知,當![]() 時,
時, ![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() 當
當![]() 時,
時, ![]() 有最大值,當
有最大值,當![]() 時,
時, ![]() 有最小值,
有最小值,
![]()
![]()
![]() 對任意
對任意![]() ,恒有
,恒有![]() ,
, ![]() .
.
構造函數![]() ,則
,則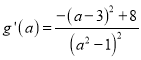 ,
,
![]()
![]() ,
, ![]()
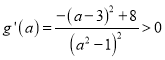 .
.
![]() 函數
函數![]() 在
在![]() 上單調增.
上單調增.
![]() ,
, ![]() .
.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案科目:高中數學 來源: 題型:
【題目】設集合![]() ,若X是
,若X是![]() 的子集,把X中所有元素的和稱為X的“容量”(規定空集的容量為0),若X的容量為奇(偶)數,則稱X為
的子集,把X中所有元素的和稱為X的“容量”(規定空集的容量為0),若X的容量為奇(偶)數,則稱X為![]() 的奇(偶)子集.
的奇(偶)子集.
(1)寫出S4的所有奇子集;
(2)求證:![]() 的奇子集與偶子集個數相等;
的奇子集與偶子集個數相等;
(3)求證:當n≥3時,![]() 的所有奇子集的容量之和等于所有偶子集的容量之和.
的所有奇子集的容量之和等于所有偶子集的容量之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市統計局就2015年畢業大學生的月收入情況調查了10000人,并根據所得數據畫出樣本的頻率分布直方圖所示,每個分組包括左端點,不包括右端點,如第一組表示![]() .
.
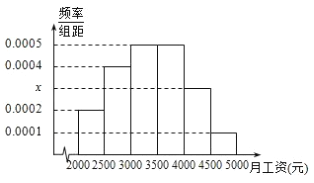
(1)求畢業大學生月收入在![]() 的頻率;
的頻率;
(2)根據頻率分布直方圖算出樣本數據的中位數;
(3)為了分析大學生的收入與所學專業、性別等方面的關系,必須按月收入再從這10000人中按分層抽樣方法抽出100人作進一步分析,則月收入在![]() 的這段應抽取多少人?
的這段應抽取多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() 和直線
和直線![]() 上的動點
上的動點![]() ,線段
,線段![]() 的垂直平分線交直線
的垂直平分線交直線![]() 于點
于點![]() ,設點
,設點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(I)求曲線![]() 的方程;
的方程;
(II)直線![]() 交
交![]() 軸于點
軸于點![]() ,交曲線
,交曲線![]() 于不同的兩點
于不同的兩點![]() ,點
,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,點
,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,求證:
,求證:![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學生在開學季準備銷售一種文具套盒進行試創業,在一個開學季內,每售出![]() 盒該產品獲利潤
盒該產品獲利潤![]() 元;未售出的產品,每盒虧損
元;未售出的產品,每盒虧損![]() 元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示,該同學為這個開學季購進了
元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示,該同學為這個開學季購進了![]() 盒該產品,以
盒該產品,以![]() (單位:盒,
(單位:盒, ![]() )表示這個開學季內的市場需求量,(單位:元)表示這個開學季內經銷該產品的利潤.
)表示這個開學季內的市場需求量,(單位:元)表示這個開學季內經銷該產品的利潤.
(1)根據直方圖估計這個開學季內市場需求量![]() 的中位數;
的中位數;
(2)將![]() 表示為
表示為![]() 的函數;
的函數;
(3)根據直方圖估計利潤不少于![]() 元的概率.
元的概率.
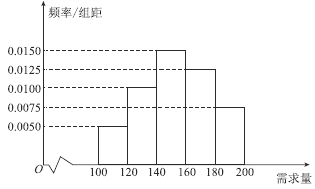
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=a,an+1=2an+![]() (a,λ∈R).
(a,λ∈R).
(1)若λ=-2,數列{an}單調遞增,求實數a的取值范圍;
(2)若a=2,試寫出an≥2對任意的n∈N*成立的充要條件,并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com