
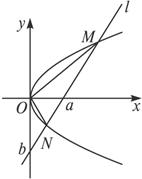
(1)寫出直線l的截距式方程;
(2)證明![]() +
+![]() =
=![]() ;
;
(3)當(dāng)a=2p時(shí),求∠MON的大小.
剖析:易知直線l的方程為![]() +
+![]() =1,欲證
=1,欲證![]() +
+![]() =
=![]() ,即求
,即求![]() 的值,為此只需求直線l與拋物線y2=2px交點(diǎn)的縱坐標(biāo).由根與系數(shù)的關(guān)系易得y1+y2、y1y2的值,進(jìn)而證得
的值,為此只需求直線l與拋物線y2=2px交點(diǎn)的縱坐標(biāo).由根與系數(shù)的關(guān)系易得y1+y2、y1y2的值,進(jìn)而證得![]() +
+![]() =
=![]() .由
.由![]() ·
·![]() =0易得∠MON=90°.亦可由kOM·kON=-1求得∠MON=90°.
=0易得∠MON=90°.亦可由kOM·kON=-1求得∠MON=90°.
(1)解:直線l的截距式方程為![]() +
+![]() =1. ①
=1. ①
(2)證明:由①及y2=2px消去x可得by2+2pay-2pab=0. ②
點(diǎn)M、N的縱坐標(biāo)y1、y2為②的兩個(gè)根,故y1+y2=![]() ,y1y2=-2pa.
,y1y2=-2pa.
所以![]() +
+![]() =
=![]() =
=![]() =
=![]() .
.
(3)解:設(shè)直線OM、ON的斜率分別為k1、k2,
則k1=![]() ,k2=
,k2=![]() .
.
當(dāng)a=2p時(shí),由(2)知,y1y2=-2pa=-4p2,
由y12=2px1,y22=2px2,相乘得
(y1y2)2=4p2x1x2,
x1x2=![]() =
=![]() =4p2,因此k1k2=
=4p2,因此k1k2=![]() =
=![]() =-1.
=-1.
所以O(shè)M⊥ON,即∠MON=90°.
講評(píng):本題主要考查直線、拋物線等基本知識(shí),考查運(yùn)用解析幾何的方法分析問題和解決問題的能力.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
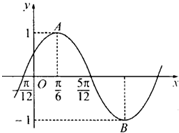 如圖是函數(shù)y=sin(ωx+φ)的圖象的一部分,A,B是圖象上的一個(gè)最高點(diǎn)和一個(gè)最低點(diǎn),O為坐標(biāo)原點(diǎn),則
如圖是函數(shù)y=sin(ωx+φ)的圖象的一部分,A,B是圖象上的一個(gè)最高點(diǎn)和一個(gè)最低點(diǎn),O為坐標(biāo)原點(diǎn),則| OA |
| OB |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
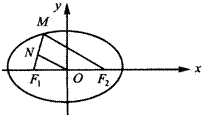 如圖,橢圓
如圖,橢圓| x2 |
| 25 |
| y2 |
| 9 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
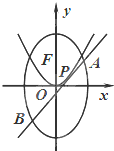 已知點(diǎn)是F拋物線C 1:x2=4y與橢圓C 2:
已知點(diǎn)是F拋物線C 1:x2=4y與橢圓C 2:| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
| 20 |
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
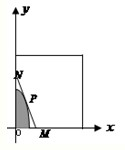 某建筑公司要在一塊寬大的矩形地面(如圖所示)上進(jìn)行開發(fā)建設(shè),陰影部分為一公共設(shè)施建設(shè)不能開發(fā),且要求用欄柵隔開(欄柵要求在一直線上),公共設(shè)施邊界為曲線f(x)=1-
某建筑公司要在一塊寬大的矩形地面(如圖所示)上進(jìn)行開發(fā)建設(shè),陰影部分為一公共設(shè)施建設(shè)不能開發(fā),且要求用欄柵隔開(欄柵要求在一直線上),公共設(shè)施邊界為曲線f(x)=1-| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com