
【題目】“地?cái)偨?jīng)濟(jì)”是李克強(qiáng)總理在本屆政府工作報(bào)告中向全國(guó)人民發(fā)出的口號(hào),某生產(chǎn)企業(yè)積極響應(yīng)號(hào)召,大力研發(fā)新產(chǎn)品,為了對(duì)新研發(fā)的一批產(chǎn)品進(jìn)行合理定價(jià),將該產(chǎn)品按事先擬定的價(jià)格進(jìn)行試銷,得到一組銷售數(shù)據(jù)![]() (
(![]() ,2,3,4,5,6),如表所示:
,2,3,4,5,6),如表所示:
試銷單價(jià)x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
產(chǎn)品銷量y(件) | q | 84 | 83 | 80 | 75 | 68 |
已知![]() ,
,![]() ,
,![]()
(1)試求q,若變量x,y具有線性相關(guān)關(guān)系,求產(chǎn)品銷量y(件)關(guān)于試銷單價(jià)x(元)的線性回歸方程![]() ;
;
(2)用![]() 表示用(1)中所求的線性回歸方程得到的與
表示用(1)中所求的線性回歸方程得到的與![]() 對(duì)應(yīng)的產(chǎn)品銷量的估計(jì)值.當(dāng)銷售數(shù)據(jù)
對(duì)應(yīng)的產(chǎn)品銷量的估計(jì)值.當(dāng)銷售數(shù)據(jù)![]() 對(duì)應(yīng)的殘差的絕對(duì)值
對(duì)應(yīng)的殘差的絕對(duì)值![]() 時(shí),則將銷售數(shù)據(jù)
時(shí),則將銷售數(shù)據(jù)![]() 稱為一個(gè)“好數(shù)據(jù)”.現(xiàn)從6個(gè)銷售數(shù)據(jù)中任取3個(gè),求“好數(shù)據(jù)”個(gè)數(shù)
稱為一個(gè)“好數(shù)據(jù)”.現(xiàn)從6個(gè)銷售數(shù)據(jù)中任取3個(gè),求“好數(shù)據(jù)”個(gè)數(shù)![]() 的分布列和數(shù)學(xué)期望
的分布列和數(shù)學(xué)期望![]() .
.
(參考公式:線性回歸方程中![]() ,
,![]() 的最小二乘估計(jì)分別為
的最小二乘估計(jì)分別為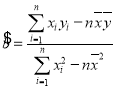 ,
,![]() )
)
【答案】(1)![]() ,
,![]() ;(2)分布列見解析,
;(2)分布列見解析,![]() .
.
【解析】
(1)由![]() ,可求q,利用
,可求q,利用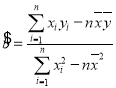 結(jié)合表中數(shù)據(jù)求出
結(jié)合表中數(shù)據(jù)求出![]() ,再利用回歸直線過樣本中心點(diǎn)求出
,再利用回歸直線過樣本中心點(diǎn)求出![]() ,從而求出回歸直線方程.
,從而求出回歸直線方程.
(2)根據(jù)(1)中的線性回歸方程求出滿足題意的“好數(shù)據(jù)”個(gè)數(shù),從而可得![]() 的所有可能取值為0,1,2,3,利用超幾何分布求出分布列,由分布列即可求出期望.
的所有可能取值為0,1,2,3,利用超幾何分布求出分布列,由分布列即可求出期望.
(1)![]() ,即
,即![]() ,求得
,求得![]() .
.
![]()
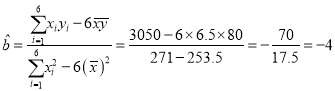 ,
,![]() ,
,
所以所求的線性回歸方程為![]() .
.
(2)利用(1)中所求的線性回歸方程![]() 可得:
可得:
當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() ;
;
當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() .
.
與銷售數(shù)據(jù)對(duì)比可知滿足![]() (
(![]() ,2,…,6)的共有3個(gè)“好數(shù)據(jù)”:
,2,…,6)的共有3個(gè)“好數(shù)據(jù)”:
![]() 、
、![]() 、
、![]() .
.
于是![]() 的所有可能取值為0,1,2,3.
的所有可能取值為0,1,2,3.
![]() ;
;![]() ;
;
![]() ;
;![]() ,
,
∴![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
于是![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某高中數(shù)學(xué)建模興趣小組的同學(xué)為了研究所在地區(qū)男高中生的身高與體重的關(guān)系,從若干個(gè)高中男學(xué)生中抽取了1000個(gè)樣本,得到如下數(shù)據(jù).
數(shù)據(jù)一:身高在![]() (單位:
(單位:![]() )的體重頻數(shù)統(tǒng)計(jì)
)的體重頻數(shù)統(tǒng)計(jì)
體重 ( |
|
|
|
|
|
|
|
|
人數(shù) | 20 | 60 | 100 | 100 | 80 | 20 | 10 | 10 |
數(shù)據(jù)二:身高所在的區(qū)間含樣本的個(gè)數(shù)及部分?jǐn)?shù)據(jù)
身高 |
|
|
|
|
|
平均體重
| 45 | 53.6 | 60 | 75 |
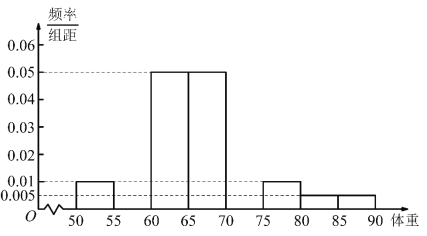
(1)依據(jù)數(shù)據(jù)一將上面男高中生身高在![]() (單位:
(單位:![]() )體重的頻率分布直方圖補(bǔ)充完整,并利用頻率分布直方圖估計(jì)身高在
)體重的頻率分布直方圖補(bǔ)充完整,并利用頻率分布直方圖估計(jì)身高在![]() (單位:
(單位:![]() )的中學(xué)生的平均體重;(保留小數(shù)點(diǎn)后一位)
)的中學(xué)生的平均體重;(保留小數(shù)點(diǎn)后一位)
(2)依據(jù)數(shù)據(jù)一、二,計(jì)算身高(取值為區(qū)間中點(diǎn))和體重的相關(guān)系數(shù)約為0.99,能否用線性回歸直線來刻畫中學(xué)生身高與體重的相關(guān)關(guān)系,請(qǐng)說明理由;若能,求出該回歸直線方程;
(3)說明殘差平方和或相關(guān)指數(shù)![]() 與線性回歸模型擬合效果之間關(guān)系.(只需寫出結(jié)論,不需要計(jì)算)
與線性回歸模型擬合效果之間關(guān)系.(只需寫出結(jié)論,不需要計(jì)算)
參考公式: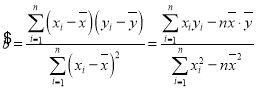 ,
,![]() .
.
參考數(shù)據(jù):(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ;(4)
;(4)![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() ,四點(diǎn)
,四點(diǎn)![]() ,
,![]() ,
,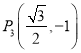 ,
,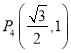 中恰有三點(diǎn)在橢圓
中恰有三點(diǎn)在橢圓![]() 上,拋物線
上,拋物線![]() 焦點(diǎn)到準(zhǔn)線的距離為
焦點(diǎn)到準(zhǔn)線的距離為![]() .
.
(1)求橢圓![]() 、拋物線
、拋物線![]() 的方程;
的方程;
(2)過橢圓![]() 右頂點(diǎn)Q的直線
右頂點(diǎn)Q的直線![]() 與拋物線
與拋物線![]() 交于點(diǎn)A、B,射線
交于點(diǎn)A、B,射線![]() 、
、![]() 分別交橢圓
分別交橢圓![]() 于點(diǎn)
于點(diǎn)![]() 、
、![]() .
.
(i)證明:![]() 為定值;
為定值;
(ii)求![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將直角三角形![]() 沿斜邊上的高
沿斜邊上的高![]() 折成
折成![]() 的二面角,已知直角邊
的二面角,已知直角邊![]() ,那么下面說法正確的是_________.
,那么下面說法正確的是_________.
(1) 平面![]() 平面
平面![]() (2)四面體
(2)四面體![]() 的體積是
的體積是![]()
(3)二面角![]() 的正切值是
的正切值是![]() (4)
(4)![]() 與平面
與平面![]() 所成角的正弦值是
所成角的正弦值是![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為改善環(huán)境,節(jié)約資源,我國(guó)自2019年起在全國(guó)地級(jí)及以上城市全面啟動(dòng)生活垃圾分類,垃圾分類已成為一種潮流.某市一小區(qū)的主管部門為了解居民對(duì)垃圾分類的認(rèn)知是否與其受教育程度有關(guān),對(duì)該小區(qū)居民進(jìn)行了隨機(jī)抽樣調(diào)查,得到如下統(tǒng)計(jì)數(shù)據(jù)的列聯(lián)表:
知道如何對(duì)垃圾進(jìn)行分類 | 不知道如何對(duì)垃圾進(jìn)行分類 | 合計(jì) | |
未受過高等教育 |
| 10 |
|
受過高等教育 |
|
|
|
合計(jì) |
|
| 50 |
(1)求列聯(lián)表中的![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值,并估計(jì)該小區(qū)受過高等教育的居民知道如何對(duì)垃圾進(jìn)行分類的概率;
的值,并估計(jì)該小區(qū)受過高等教育的居民知道如何對(duì)垃圾進(jìn)行分類的概率;
(2)根據(jù)列聯(lián)表判斷能否有![]() 的把握認(rèn)為該小區(qū)居民對(duì)垃圾分類的認(rèn)知與其受教育程度有關(guān)?
的把握認(rèn)為該小區(qū)居民對(duì)垃圾分類的認(rèn)知與其受教育程度有關(guān)?
參考數(shù)據(jù)及公式:
|
|
|
|
|
|
|
|
|
|
|
|
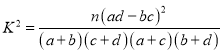 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為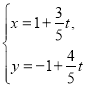 (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)
為參數(shù)),以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
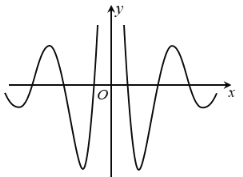
【題目】我們可從這個(gè)商標(biāo)![]() 中抽象出一個(gè)如圖靠背而坐的兩條優(yōu)美的曲線,下列函數(shù)中大致可“完美”局部表達(dá)這對(duì)曲線的函數(shù)是( )
中抽象出一個(gè)如圖靠背而坐的兩條優(yōu)美的曲線,下列函數(shù)中大致可“完美”局部表達(dá)這對(duì)曲線的函數(shù)是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,點(diǎn)E在線段
,點(diǎn)E在線段![]() 上,且
上,且![]() .
.
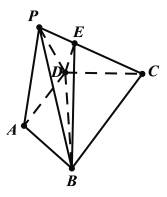
(1)證明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形![]() 與矩形
與矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 上一點(diǎn).
上一點(diǎn).
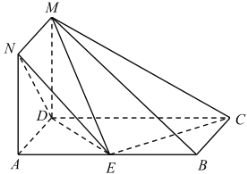
(1)若點(diǎn)![]() 是
是![]() 的中點(diǎn),求證:
的中點(diǎn),求證:![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成的線面角的大小為
所成的線面角的大小為![]() ,求
,求![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com