【題目】已知函數
.
(1)若
在
上單調遞減，求
的取值范圍；
(2)若在
處取得極值，判斷當
時，存在幾條切線與直線
平行，請說明理由；
(3)若有兩個極值點
，求證：
.
【答案】(Ⅰ)
；(Ⅱ)答案見解析；(Ⅲ)證明見解析.
【解析】
(Ⅰ)由題意可得
恒成立 ，構造函數，令
,由導函數的解析式可知
在
遞增,在
遞減, 據此計算可得實數a的取值范圍.
(Ⅱ) 由
在
處取得極值可得
.原問題等價于求解
在區間
內解的個數，結合導函數的解析式研究函數的單調性和函數在特殊點處的函數值即可確定切線的條數.而事實情況下檢驗時函數不存在極值點，所以不存在滿足題意的實數
，也不存在滿足題意的切線.
(Ⅲ)若函數有兩個極值點
,不妨設
，易知
,結合函數的解析式和零點的性質即可證得題中的不等式.
(Ⅰ)由已知,
恒成立
令,
則
,
,令
,解得:
,令
,解得:
,
故在遞增,在遞減,
，由
恒成立可得
.
即當在
上單調遞減時,的取值范圍是
.
(Ⅱ)在處取得極值，則
，可得.
令
，即 .
設
，則
.
故
在上單調遞增，在
上單調遞減，
注意到
，
，
則方程在內只有一個實數根，
即當
時，只有一條斜率為
且與函數圖像相切的直線.
但事實上，若，則
，
，
故函數
在區間上單調遞增，在區間上單調遞減，
且
，故函數在區間上恒成立，
函數在區間上單調遞減，即函數不存在極值點，
即不存在滿足題意的實數，也不存在滿足題意的切線.
(Ⅲ)若函數有兩個極值點,不妨設，
由(Ⅰ)可知,且：
①,
②,
由①-②得:
,
即
,
由①+②得:
,
.
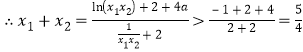閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】某精準扶貧幫扶單位，為幫助定點扶貧村真正脫貧，堅持扶貧同扶智相結合，幫助精準扶貧戶利用互聯網電商渠道銷售當地特產蘋果.蘋果單果直徑不同單價不同，為了更好的銷售，現從該精準扶貧戶種植的蘋果樹上隨機摘下了50個蘋果測量其直徑，經統計，其單果直徑分布在區間[50，95]內（單位：
），統計的莖葉圖如圖所示：
（Ⅰ）從單果直徑落在[72，80）的蘋果中隨機抽取3個，求這3個蘋果單果直徑均小于76的概率；
（Ⅱ）以此莖葉圖中單果直徑出現的頻率代表概率.直徑位于[65，90）內的蘋果稱為優質蘋果，對于該精準扶貧戶的這批蘋果，某電商提出兩種收購方案：
方案
：所有蘋果均以5元/千克收購；
方案
：從這批蘋果中隨機抽取3個蘋果，若都是優質蘋果，則按6元/干克收購；若有1個非優質蘋果，則按5元/千克收購；若有2個非優質蘋果，則按4.5元/千克收購；若有3個非優質蘋果，則按4元/千克收購.
請你通過計算為該精準扶貧戶推薦收益最好的方案.
查看答案和解析>>
科目：高中數學 來源： 題型：
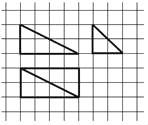
【題目】我國古代數學名著《九章算術商功》中闡述：“斜解立方，得兩塹堵．斜解塹堵，其一為陽馬，一為鱉臑．陽馬居二，鱉臑居一，不易之率也．合兩鱉臑三而一，驗之以棊，其形露矣．”若稱為“陽馬”的某幾何體的三視圖如圖所示，圖中網格紙上小正方形的邊長為1，對該幾何體有如下描述：
①四個側面都是直角三角形；
②最長的側棱長為
；
③四個側面中有三個側面是全等的直角三角形；
④外接球的表面積為24π．
其中正確的描述為____．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設拋物線
：
的焦點為
，直線
與交于
，
兩點，
的面積為
.
（1）求的方程；
（2）若
，
是上的兩個動點，
，試問：是否存在定點
，使得
？若存在，求的坐標，若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在多面體
中，四邊形
是正方形，平面
平面，
.
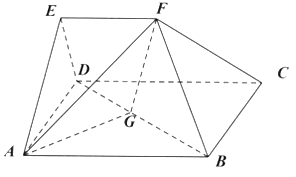
（1）求證：
平面
；
（2）在線段
上是否存在點
，使得平面
與平面
所成的銳二面角的大小為
，若存在，求出
的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
O
中，直線
與拋物線
＝2相交于A、B兩點．
（1）求證：命題“如果直線過點T（3，0），那么
＝3”是真命題；
（2）寫出（1）中命題的逆命題，判斷它是真命題還是假命題，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖在四棱錐
中,底面
為矩形,
,
,平面
平面,
為等腰直角三角形,且
,
為底面的中心.
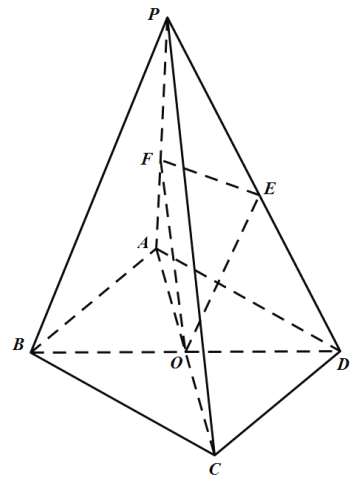
(1)求異面直線
與
所成角的余弦值;
(2)若
為
中點,
在棱
上,若
,
,且二面角
的正弦值為
,求實數
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校高一年級學生某次身體素質體能測試的原始成績采用百分制,已知所有這些學生的原始成績均分布在
內,發布成績使用等級制各等級劃分標準見下表,規定： 
、
、
三級為合格等級, 
為不合格等級.
百分制 |
|
|
|
|
等級 |
|
|
|
|
為了解該校高一年級學生身體素質情況,從中抽取了
名學生的原始成績作為樣本進行統計,按照
的分組作出頻率分布直方圖如圖
所示,樣本中分數在
分及以上的所有數據的莖葉圖如圖
所示.
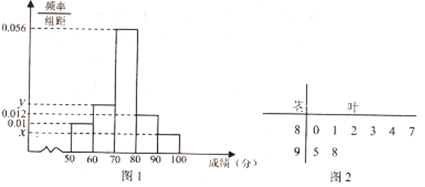
（1）求
和頻率分布直方圖中的
的值；
（2）根據樣本估計總體的思想，以事件發生的頻率作為相應事件發生的概率，若在該校高一學生任選
人,求至少有
人成績是合格等級的概率；
（3）在選取的樣本中,從
、
兩個等級的學生中隨機抽取了
名學生進行調研,記
表示所抽取的
名學生中為
等級的學生人數,求隨機變量
的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題中的真命題是（ ）
A. 若
，則向量
與
的夾角為鈍角
B. 若
，則
C. 若命題“
是真命題”，則命題“
是真命題”
D. 命題“
，
”的否定是“
，
”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
