
【題目】為了積極穩妥疫情期間的復學工作,市教育局抽調5名機關工作人員去某街道3所不同的學校開展駐點服務,每個學校至少去1人,若甲、乙兩人不能去同一所學校,則不同的分配方法種數為___________.
【答案】114
【解析】
先排甲乙,將最后的三人分成四種情況:(1)三人一起去第三所學校,(2)兩個人去第三所學校,另一個人到前兩所學校中任意一所,(3)一人到第三所學校,另兩個人一起到前兩所學校中的任意一所,(4)一人到第三所學校,另兩人分別到前兩所學校中的任意一所.再分別計算即可得到答案.
分四種情況:
(1)安排甲去一所學校共有![]() 種方法,
種方法,
安排乙到第二所學校共有![]() 種方法,
種方法,
余下三人去第三所學校共有![]() 種方法,共有
種方法,共有![]() 種方法.
種方法.
(2)安排甲去一所學校共有![]() 種方法,
種方法,
安排乙到第二所學校共有![]() 種方法,
種方法,
余下的三人中兩人一起去第三所學校有![]() 種方法,
種方法,
另一個人去前兩所學校中任意一所共有![]() 種方法,
種方法,
共有![]() 種方法.
種方法.
(3)安排甲去一所學校共有![]() 種方法,
種方法,
安排乙到第二所學校共有![]() 種方法,
種方法,
余下的三人中一人去第三所學校有![]() 種方法,
種方法,
另外兩人一起去前兩所學校中任意一所共有![]() 種方法,
種方法,
共有![]() 種方法.
種方法.
(4)安排甲去一所學校共有![]() 種方法,
種方法,
安排乙到第二所學校共有![]() 種方法,
種方法,
余下的三人中一人去第三所學校有![]() 種方法,
種方法,
另外兩人分別去前兩所學校中任意一所共有![]() 種方法,
種方法,
共有![]() 種方法.
種方法.
綜上共有![]() 種方法.
種方法.
故答案為:![]()


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:高中數學 來源: 題型:
【題目】如圖,![]() 是拋物線
是拋物線![]() 的焦點,過點
的焦點,過點![]() 且與坐標軸不垂直的直線交拋物線于
且與坐標軸不垂直的直線交拋物線于![]() 、
、![]() 兩點,交拋物線的準線于點
兩點,交拋物線的準線于點![]() ,其中
,其中![]() ,
,![]() .過點
.過點![]() 作
作![]() 軸的垂線交拋物線于點
軸的垂線交拋物線于點![]() ,直線
,直線![]() 交拋物線于點
交拋物線于點![]() .
.
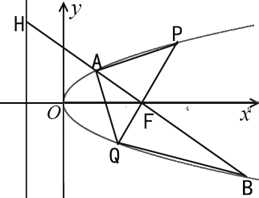
(1)求![]() 的值;
的值;
(2)求四邊形![]() 的面積
的面積![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年1月3日嫦娥四號探測器成功實現人類歷史上首次月球背面軟著陸,我國航天事業取得又一重大成就,實現月球背面軟著陸需要解決的一個關鍵技術問題是地面與探測器的通訊聯系.為解決這個問題,發射了嫦娥四號中繼星“鵲橋”,鵲橋沿著圍繞地月拉格朗日![]() 點的軌道運行.
點的軌道運行.![]() 點是平衡點,位于地月連線的延長線上.設地球質量為M1,月球質量為M2,地月距離為R,
點是平衡點,位于地月連線的延長線上.設地球質量為M1,月球質量為M2,地月距離為R,![]() 點到月球的距離為r,根據牛頓運動定律和萬有引力定律,r滿足方程:
點到月球的距離為r,根據牛頓運動定律和萬有引力定律,r滿足方程:
![]() .
.
設![]() ,由于
,由于![]() 的值很小,因此在近似計算中
的值很小,因此在近似計算中![]() ,則r的近似值為
,則r的近似值為
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“雜交水稻之父”袁隆平一生致力于雜交水稻技術的研究、應用與推廣,發明了“三系法”秈型雜交水稻,成功研究出“兩系法”雜交水稻,創建了超級雜交稻技術體系,為我國糧食安全、農業科學發展和世界糧食供給做出了杰出貢獻;某雜交水稻種植研究所調查某地水稻的株高,得出株高(單位:cm)服從正態分布,其密度曲線函數為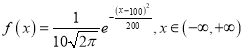 ,則下列說法正確的是( )
,則下列說法正確的是( )
A.該地水稻的平均株高為100cm
B.該地水稻株高的方差為10
C.隨機測量一株水稻,其株高在120cm以上的概率比株高在70cm以下的概率大
D.隨機測量一株水稻,其株高在(80,90)和在(100,110)(單位:cm)的概率一樣大
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線![]() ,設直線
,設直線![]() 經過點
經過點![]() 且與拋物線
且與拋物線![]() 相交于
相交于![]() 兩點,拋物線
兩點,拋物線![]() 在
在![]() 、
、![]() 兩點處的切線相交于點
兩點處的切線相交于點![]() ,直線
,直線![]() ,
,![]() 分別與
分別與![]() 軸交于
軸交于![]() 、
、![]() 兩點.
兩點.

(1)求點![]() 的軌跡方程
的軌跡方程
(2)當點![]() 不在
不在![]() 軸上時,記
軸上時,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題共l4分)
已知函數f(x)=![]() x +
x +![]() , h(x)=
, h(x)=![]() .
.
(I)設函數F(x)=f(x)一h(x),求F(x)的單調區間與極值;
(Ⅱ)設a∈R,解關于x的方程log4[![]() ]=1og2h(a-x)一log2h (4-x);
]=1og2h(a-x)一log2h (4-x);
(Ⅲ)試比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com