
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .以
.以![]() ,
,![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() ,連接
,連接![]() 和
和![]() .
.
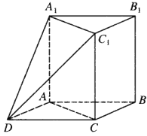
(1)求證:![]() 平面
平面![]() ;
;
(2)線段![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使平面
,使平面![]() 與平面
與平面![]() 垂直?若存在,求出
垂直?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
【答案】(1)證明見解析;(2)存在,![]()
【解析】
(1)根據(jù)線面平行的判定定理即可證明;
(2)先根據(jù)圖形建立空間直角坐標(biāo)系,設(shè)出點(diǎn)![]() 的坐標(biāo),根據(jù)兩平面垂直得到二面角的平面角為
的坐標(biāo),根據(jù)兩平面垂直得到二面角的平面角為![]() ,再分別算出兩平面的法向量,使兩個法向量的夾角的余弦值為0,即可求解.
,再分別算出兩平面的法向量,使兩個法向量的夾角的余弦值為0,即可求解.
解:(1)
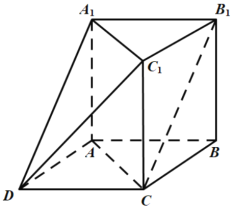
證明:如圖所示:連接![]() ,
,
∵四邊形![]() 為平行四邊形,
為平行四邊形,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴四邊形![]() 為平行四邊形,
為平行四邊形,
∴![]() ,
,
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)假設(shè)存在點(diǎn)![]() ,使平面
,使平面![]() 與平面
與平面![]() 垂直,
垂直,
則平面![]() 與平面
與平面![]() 的二面角為直二面角,
的二面角為直二面角,
設(shè)平面![]() 與平面
與平面![]() 的二面角的平面角為
的二面角的平面角為![]() ,則
,則![]() ,
,
如圖所示:以![]() 為坐標(biāo)原點(diǎn),分別以射線
為坐標(biāo)原點(diǎn),分別以射線![]() ,
,![]() ,
,![]() 為
為![]() ,
,![]() ,
,![]() 軸的正方向,建立空間直角坐標(biāo)系,
軸的正方向,建立空間直角坐標(biāo)系,
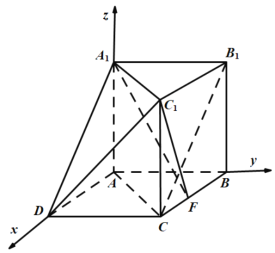
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵點(diǎn)![]() 在
在![]() 上,∴設(shè)點(diǎn)
上,∴設(shè)點(diǎn)![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
分別設(shè)平面![]() 和平面
和平面![]() 的法向量為
的法向量為![]() ,
,![]() ,
,
則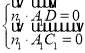 ,
,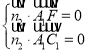 ,
,
即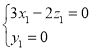 ,
,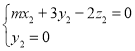 ,
,
∴取![]() ,
,![]() ,
,
則![]() ,
,
∴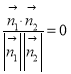 ,即
,即![]() ,∴
,∴![]() ,
,
即![]() ,∴
,∴![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,四邊形![]() 為菱形,
為菱形,![]() ,二面角
,二面角![]() 為直二面角,點(diǎn)
為直二面角,點(diǎn)![]() 是棱
是棱![]() 的中點(diǎn).
的中點(diǎn).
(Ⅰ)求證:![]() ;
;
(Ⅱ)若![]() ,當(dāng)二面角
,當(dāng)二面角![]() 的余弦值為
的余弦值為![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】十九大以來,某貧困地區(qū)扶貧辦積極貫徹落實(shí)國家精準(zhǔn)扶貧的政策要求,帶領(lǐng)廣大農(nóng)村地區(qū)人民群眾脫貧奔小康.經(jīng)過不懈的奮力拼搏,新農(nóng)村建設(shè)取得巨大進(jìn)步,農(nóng)民年收入也逐年增加,為了制定提升農(nóng)民收入、實(shí)現(xiàn)2020年脫貧的工作計劃,該地扶貧辦統(tǒng)計了2019年50位農(nóng)民的年收入并制成如下頻率分布直方圖:
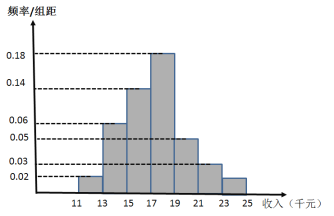
(1)根據(jù)頻率分布直方圖,估計50位農(nóng)民的平均年收入![]() (單位:千元);(同一組數(shù)據(jù)用該組數(shù)據(jù)區(qū)間的中點(diǎn)值表示);
(單位:千元);(同一組數(shù)據(jù)用該組數(shù)據(jù)區(qū)間的中點(diǎn)值表示);
(2)由頻率分布直方圖,可以認(rèn)為該貧困地區(qū)農(nóng)民年收入X服從正態(tài)分布![]() ,其中
,其中![]() 近似為年平均收入
近似為年平均收入![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() ,經(jīng)計算得
,經(jīng)計算得![]() =6.92,利用該正態(tài)分布,求:
=6.92,利用該正態(tài)分布,求:
①在扶貧攻堅工作中,若使該地區(qū)約有占總農(nóng)民人數(shù)的![]() 的農(nóng)民的年收入高于扶貧辦制定的最低年收入標(biāo)準(zhǔn),則最低年收入標(biāo)準(zhǔn)大約為多少千元?
的農(nóng)民的年收入高于扶貧辦制定的最低年收入標(biāo)準(zhǔn),則最低年收入標(biāo)準(zhǔn)大約為多少千元?
②為了調(diào)研“精準(zhǔn)扶貧,不落一人”的政策要求落實(shí)情況,扶貧辦隨機(jī)走訪了1000位農(nóng)民.若每位農(nóng)民的年收入互相獨(dú)立,問:這1000位農(nóng)民中的年收入不少于12.14千元的人數(shù)最有可能是多少?
附參考數(shù)據(jù):![]() ,若隨機(jī)變量X服從正態(tài)分布
,若隨機(jī)變量X服從正態(tài)分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,
中,![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),![]() ,
,![]() ,已知
,已知![]() 是以
是以![]() 為底邊,且邊
為底邊,且邊![]() 平行于
平行于![]() 軸的等腰三角形.
軸的等腰三角形.
(1)求動點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知直線![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,且與曲線
,且與曲線![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在曲線
在曲線![]() 上,且直線
上,且直線![]() 軸,點(diǎn)
軸,點(diǎn)![]() 關(guān)于點(diǎn)
關(guān)于點(diǎn)![]() 的對稱點(diǎn)為點(diǎn)
的對稱點(diǎn)為點(diǎn)![]() ,試判斷點(diǎn)
,試判斷點(diǎn)![]() 、
、![]() 、
、![]() 三點(diǎn)是否共線,并說明理由.
三點(diǎn)是否共線,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示的四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() 平面
平面![]() ,
,![]() ,M,N分別是
,M,N分別是![]() ,
,![]() 的中點(diǎn).
的中點(diǎn).

(1)求證:![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成角的余弦值為
所成角的余弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若函數(shù)![]() 有極值,求實(shí)數(shù)
有極值,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 時,若
時,若![]() 在
在![]() ,
,![]() 處導(dǎo)數(shù)相等,證明:
處導(dǎo)數(shù)相等,證明:![]() ;
;
(3)若函數(shù)![]() 在
在![]() 上有兩個零點(diǎn)
上有兩個零點(diǎn)![]() ,
,![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】互聯(lián)網(wǎng)正在改變著人們的生活方式,在日常消費(fèi)中手機(jī)支付正逐漸取代現(xiàn)金支付成為人們首選的支付方式. 某學(xué)生在暑期社會活動中針對人們生活中的支付方式進(jìn)行了調(diào)查研究. 采用調(diào)查問卷的方式對100名18歲以上的成年人進(jìn)行了研究,發(fā)現(xiàn)共有60人以手機(jī)支付作為自己的首選支付方式,在這60人中,45歲以下的占![]() ,在仍以現(xiàn)金作為首選支付方式的人中,45歲及以上的有30人.
,在仍以現(xiàn)金作為首選支付方式的人中,45歲及以上的有30人.
(1)從以現(xiàn)金作為首選支付方式的40人中,任意選取3人,求這3人至少有1人的年齡低于45歲的概率;
(2)某商家為了鼓勵人們使用手機(jī)支付,做出以下促銷活動:凡是用手機(jī)支付的消費(fèi)者,商品一律打八折. 已知某商品原價50元,以上述調(diào)查的支付方式的頻率作為消費(fèi)者購買該商品的支付方式的概率,設(shè)銷售每件商品的消費(fèi)者的支付方式都是相互獨(dú)立的,求銷售10件該商品的銷售額的數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年底,武漢發(fā)生“新型冠狀病毒”肺炎疫情,國家衛(wèi)健委緊急部署,從多省調(diào)派醫(yī)務(wù)工作者前去支援,正值農(nóng)歷春節(jié)舉家團(tuán)圓之際,他們成為“最美逆行者”.武漢市從2月7日起舉全市之力入戶上門排查確診的新冠肺炎患者疑似的新冠肺炎患者無法明確排除新冠肺炎的發(fā)熱患者和確診患者的密切接觸者等“四類”人員,強(qiáng)化網(wǎng)格化管理,不落一戶不漏一人.若在排查期間,某小區(qū)有5人被確認(rèn)為“確診患者的密切接觸者”,現(xiàn)醫(yī)護(hù)人員要對這5人隨機(jī)進(jìn)行逐一“核糖核酸”檢測,只要出現(xiàn)一例陽性,則將該小區(qū)確定為“感染高危小區(qū)”.假設(shè)每人被確診的概率均為![]() 且相互獨(dú)立,若當(dāng)
且相互獨(dú)立,若當(dāng)![]() 時,至少檢測了4人該小區(qū)被確定為“感染高危小區(qū)”的概率取得最大值,則
時,至少檢測了4人該小區(qū)被確定為“感染高危小區(qū)”的概率取得最大值,則![]() ____.
____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若數(shù)列![]() 滿足“對任意正整數(shù)
滿足“對任意正整數(shù)![]() ,都存在正整數(shù)
,都存在正整數(shù)![]() ,使得
,使得![]() ”,則稱數(shù)列
”,則稱數(shù)列![]() 具有“性質(zhì)
具有“性質(zhì)![]() ”.已知數(shù)列
”.已知數(shù)列![]() 為無窮數(shù)列.
為無窮數(shù)列.
(1)若![]() 為等比數(shù)列,且
為等比數(shù)列,且![]() ,判斷數(shù)列
,判斷數(shù)列![]() 是否具有“性質(zhì)
是否具有“性質(zhì)![]() ”,并說明理由;
”,并說明理由;
(2)若![]() 為等差數(shù)列,且公差
為等差數(shù)列,且公差![]() ,求證:數(shù)列
,求證:數(shù)列![]() 不具有“性質(zhì)
不具有“性質(zhì)![]() ”;
”;
(3)若等差數(shù)列![]() 具有“性質(zhì)
具有“性質(zhì)![]() ”,且
”,且![]() ,求數(shù)列
,求數(shù)列![]() 的通項公式
的通項公式![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com