
已知函數(shù) .
.
(Ⅰ)求 的極值;
的極值;
(II)判斷y=f(x)的圖像是否是中心對(duì)稱圖形,若是求出對(duì)稱中心并證明,否則說明理由;
(III)設(shè) 的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052113275073432175/SYS201205211329139843134269_ST.files/image003.png">,是否存在
的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052113275073432175/SYS201205211329139843134269_ST.files/image003.png">,是否存在 .當(dāng)
.當(dāng) 時(shí),
時(shí), 的取值范圍是
的取值范圍是 ?若存在,求實(shí)數(shù)
?若存在,求實(shí)數(shù) 、
、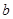 的值;若不存在,說明理由
的值;若不存在,說明理由
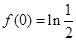 是
是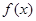 的一個(gè)極大值,
的一個(gè)極大值,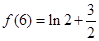 是
是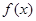 的一個(gè)極小值.
的一個(gè)極小值. 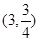
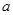 、
、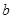 不存在
不存在
【解析】
解:(I) 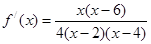 .注意到
.注意到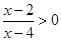 ,即
,即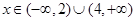 ,
,
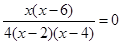 得
得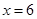 或
或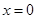 .所以當(dāng)
.所以當(dāng)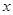 變化時(shí),
變化時(shí), 的變化情況如下表:
的變化情況如下表:
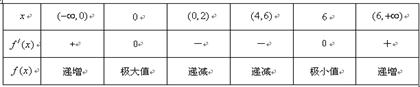
所以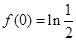 是
是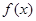 的一個(gè)極大值,
的一個(gè)極大值,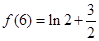 是
是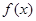 的一個(gè)極小值.
的一個(gè)極小值.
|
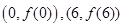 的中點(diǎn)是
的中點(diǎn)是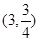 ,所以
,所以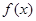 的圖象的對(duì)稱中心只可能是
的圖象的對(duì)稱中心只可能是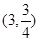 .
.
設(shè) 為
為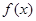 的圖象上一點(diǎn),
的圖象上一點(diǎn),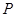 關(guān)于
關(guān)于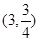 的對(duì)稱點(diǎn)是Q
的對(duì)稱點(diǎn)是Q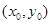 ,
,
因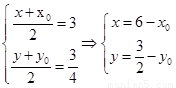 ,又
,又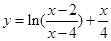
所以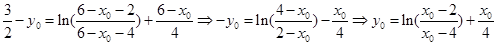 ,
,
|
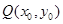 也在函數(shù)y=f(x)的圖像上。
也在函數(shù)y=f(x)的圖像上。
設(shè)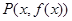 為
為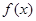 的圖象上一點(diǎn),
的圖象上一點(diǎn),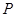 關(guān)于
關(guān)于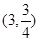 的對(duì)稱點(diǎn)是
的對(duì)稱點(diǎn)是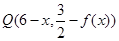 ……
……
(III) 假設(shè)存在實(shí)數(shù)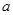 、
、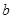 .
.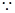
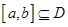 ,
,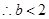 或
或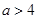 .
.
若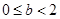 , 當(dāng)
, 當(dāng)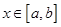 時(shí),
時(shí), 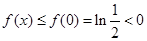 ,而
,而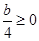
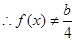 .故不可能…
.故不可能…
若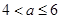 ,當(dāng)
,當(dāng)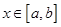 時(shí),
時(shí), 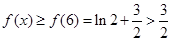 ,而
,而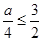
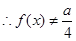 .故不可能….
.故不可能….
若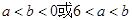 ,由
,由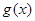 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是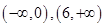 ,知
,知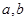 是
是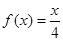 的兩個(gè)解.而
的兩個(gè)解.而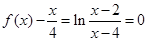 無解. 故此時(shí)
無解. 故此時(shí)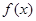 的取值范圍是不可能是
的取值范圍是不可能是 .
.
綜上所述,假設(shè)錯(cuò)誤,滿足條件的實(shí)數(shù)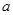 、
、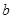 不存在.
不存在.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆江西省高三上學(xué)期第二次月考文科數(shù)學(xué)試卷(解析版) 題型:解答題
已知函數(shù)
 .
.
(1)求函數(shù) 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)若對(duì)任意 ,函數(shù)
,函數(shù) 在
在 上都有三個(gè)零點(diǎn),求實(shí)數(shù)
上都有三個(gè)零點(diǎn),求實(shí)數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年廣東省東莞市教育局教研室高三上學(xué)期數(shù)學(xué)文卷 題型:解答題
(本小題滿分 分)
分)
已知函數(shù) .
.
(1)求函數(shù)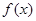 的最大值;
的最大值;
(2)在 中,
中, ,角
,角 滿足
滿足 ,求
,求 的面積.
的面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com