Question

【題目】對于函數f1（x），f2（x），h（x），如果存在實數a，b使得h（x）=af1（x）+bf2（x），那么稱h（x）為f1（x），f2（x）的生成函數.

（1）函數f1（x）=x2﹣x，f2（x）=x2+x+1，h（x）=x2﹣x+1，h（x）是否為f1（x），f2（x）的生成函數？說明理由；

（2）設f1（x）=1﹣x，f2（x）=，當a=b=1時生成函數h（x），求h（x）的對稱中心（不必證明）；

（3）設f1（x）=x，（x≥2），取a=2，b＞0，生成函數h（x），若函數h（x）的最小值是5，求實數b的值.

Answer 1

【答案】（1）不是，理由見解析；（2）（1，1）；（3）1

【解析】

（1）先假設存在，列出方程，根據方程無解，得出不存在；

（2）化簡函數式為h（x）=1﹣x++1，從而判斷函數圖象關于點（1，1）中心對稱；

（3）運用雙勾函數的圖象和性質，并通過分類討論確定函數的最值．

解：（1）根據生成函數的定義，設存在a，b使得h（x）=af1（x）+bf2（x），

則x2﹣x+1=a（x2﹣x）+b（x2+x+1）=（a+b）x2+（b﹣a）x+b，

對比兩邊的系數可知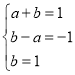，，方程無解，

所以，h（x）不是f1（x），f2（x）的生成函數；

（2）因為a=b=1，所以，h（x）=1﹣x+，

而h（x）=1﹣x+=（1﹣x）+=+1，

該函數的圖象為雙曲線，對稱中心為（1，1）；

（3）根據題意，h（x）=2x+=2（x﹣1）++2（x≥2），

根據基本不等式，2（x﹣1）+≥2，

當且僅當：x=+1時，取“=”，

因此，函數h（x）在（1， +1）上單調遞減，在（+1，+∞）上單調遞增，

故令+1=2，解得b=2，最值情況分類討論如下：

①當b∈（0，2]時，+1≤2，

所以，當x≥2/span>時，h（x）單調遞增，h（x）min=h（2）=b+4=5，解得b=1，符合題意；

②當b∈（2，+∞）時，+1＞2，

所以，當x≥2時，h（x）先減后增，h（x）min=h（+1）=2+2=5，解得b=，不合題意；

綜上：實數b的值為1．