【題目】已知橢圓C： 
的一個焦點與拋物線y2＝－4x的焦點相同，且橢圓C上一點與橢圓C的左，右焦點F1，F2構成的三角形的周長為
.
(1)求橢圓C的方程；
(2)若直線l：y＝kx＋m(k，m∈R)與橢圓C交于A，B兩點，O為坐標原點，△AOB的重心G滿足： 
，求實數m的取值范圍．
【答案】（1）
；（2）
【解析】試題分析：(1)利用與拋物線有公共焦點、橢圓的定義及幾何要素間的等量關系進行求解；(2)聯立直線和橢圓的方程，得到關于
的一元二次方程，利用根與系數的關系、三角形的重心性質和平面向量的數量積運算進行求解.
試題解析：(1)依題意得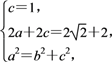
即
所以橢圓C的方程為
＋y2＝1.
(2)設A(x1，y1)，B(x2，y2)，
聯立得方程組
消去y并整理得(1＋2k2)x2＋4kmx＋2m2－2＝0，
則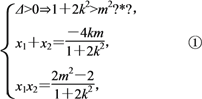
設△AOB的重心為G(x，y)，
由
·
＝－
，
可得x2＋y2＝
.②
由重心公式可得G(
，
)，
代入②式，整理可得(x1＋x2)2＋(y1＋y2)2＝4(x1＋x2)2＋[k(x1＋x2)＋2m]2＝4，③
將①式代入③式并整理，
得m2＝
，
代入(*)得k≠0，
則m2＝
＝1＋
＝1＋
.
∵k≠0，∴t＝
>0，∴t2＋4t>0，
∴m2>1，∴m∈(－∞，－1)∪(1，＋∞)．
同步練習強化拓展系列答案科目：高中數學 來源： 題型：
【題目】某化工廠引進一條先進生產線生產某種化工產品，其生產的總成本
（萬元）與年產量
（噸）之間的函數關系式可以近似的表示為
，已知此生產線年產量最大為
噸．
（1）求年產量為多少噸時，生產每噸產品的平均成本最低，并求最低成本；
（2）若每噸產品平均出廠價為40萬元，那么當年產量為多少噸時，可以獲得最大利潤？最大利潤是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，將曲線
上的所有點橫坐標伸長為原來的
倍，縱坐標伸長為原來的2倍后，得到曲線
，在以
為極點， 
軸正半軸為極軸的極坐標系中，直線
的極坐標方程是
.
（1）寫出曲線
的參數方程和直線
的直角坐標方程；
（2）在曲線
上求一點
，使點
到直線
的距離
最大，并求出此最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
的左焦點為F(－1，0)，經過點F的直線l0與橢圓交于A，B兩點.當直線l0⊥x軸時，|AB|＝
.
(1)求橢圓C的方程；
(2)作直線l⊥x軸，分別過A，B作AA1⊥l，垂足為A1，BB1⊥l，垂足為B1，且△A1FB1是直角三角形.問：是否存在直線l使得∠A1FO＝2∠B1FO？若存在，求出直線l的方程；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，C1的參數方程為
(t為參數)，在以坐標原點為極點，x軸正半軸為極軸的極坐標系中，C2的極坐標方程ρ2－2ρcos θ－3＝0.
(Ⅰ)說明C2是哪種曲線，并將C2的方程化為普通方程；
(Ⅱ)C1與C2有兩個公共點A，B，定點P的極坐標
，求線段AB的長及定點P到A，B兩點的距離之積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等差數列{an}的首項a1＝1，公差d＞0.且a2，a5，a14分別是等比數列{bn}的b2，b3，b4.
(1)求數列{an}與{bn}的通項公式；
(2)設數列{cn}對任意自然數n均有
成立，求c1＋c2＋…＋c2016的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在數列{an}中，a1＝1，a2＝2，數列{anan＋1}是公比為q (q>0)的等比數列，則數列{an}的前2n項和S2n＝____________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知拋物線x2＝y，點
，拋物線上的點
，過點B作直線AP的垂線，垂足為Q.
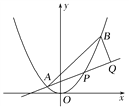
(1)求直線AP斜率的取值范圍；
(2)求|PA|·|PQ|的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
