Question

【題目】已知函數(shù)，．

（Ⅰ）若在內(nèi)單調(diào)遞減，求實數(shù)的取值范圍；

（Ⅱ）若函數(shù)有兩個極值點分別為，，證明：．

Answer 1

【答案】（Ⅰ）（Ⅱ）見證明

【解析】

（I）先求得函數(shù)的導數(shù)，根據(jù)函數(shù)在上的單調(diào)性列不等式，分離常數(shù)后利用構(gòu)造函數(shù)法求得的取值范圍.（II）將極值點代入導函數(shù)列方程組，將所要證明的不等式轉(zhuǎn)化為證明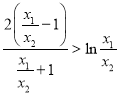，利用構(gòu)造函數(shù)法證得上述不等式成立.

（I）．

∴在內(nèi)單調(diào)遞減，

∴在內(nèi)恒成立，

即在內(nèi)恒成立．

令，則，

∴當時，，即在內(nèi)為增函數(shù)；

當時，，即在內(nèi)為減函數(shù)．

∴的最大值為，

∴

（Ⅱ）若函數(shù)有兩個極值點分別為，，

則在內(nèi)有兩根，，

由（I），知．

由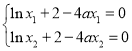，兩式相減，得．

不妨設，

∴要證明，只需證明．

即證明，亦即證明．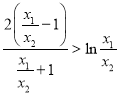

令函數(shù)．

∴，即函數(shù)在內(nèi)單調(diào)遞減．

∴時，有，∴．

即不等式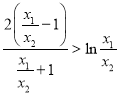成立．

綜上，得．