【題目】如圖，在市中心有一矩形空地
．市政府欲將它改造成綠化景觀帶，具體方案如下：在邊
上分別取點M，N，在三角形
內建造假山，在以
為直徑的半圓內建造噴泉，其余區(qū)域栽種各種觀賞類植物．
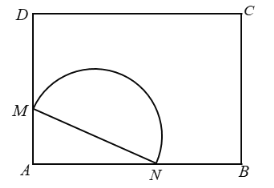
（1）若假山區(qū)域面積為
，求噴泉區(qū)域面積的最小值；
（2）若
，求假山區(qū)域面積的最大值．
【答案】（1）
；（2）
.
【解析】
（1）設
，半圓的直徑
，根據假山區(qū)域面積為
，找到
與
的關系，再表示出噴泉區(qū)域面積，求最值，注意驗證半圓是否在矩形空地
內，即驗證是否能取到最小值；
（2）由（1）根據以
為直徑的半圓區(qū)域在矩形廣場內，求得的范圍，再將假山區(qū)域面積用表示出來，再求最值.
解：（1）設，半圓的直徑，半圓的圓心為O．
在直角三角形
中，
，所以
．
因為假山區(qū)域面積為，
所以
所以
，所以噴泉區(qū)域面積
，
當且僅當
，即
時取等號．此時
．
因為點O到
的距離
，點O到
的距離
，
所以
，即
，
，即
．
所以以為直徑的半圓區(qū)域一定在矩形廣場內．
所以當時，
取得最小值．
噴泉區(qū)域面積的最小值為．
（2）由（1）知，若
，則
．
所以點O到的距離
，
點O到的距離
，
因為以為直徑的半圓區(qū)域在矩形廣場內，
所以
即
所以
．
又因為
，所以
．
所以假山區(qū)域面積
，
因為，所以
，
所以當
時，假山區(qū)域面積的最大值為．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖1，在等腰梯形
中，
，
，
，
為
的中點.現分別沿
，
將
和
折起，點
折至點
，點
折至點
，使得平面
平面
，平面
平面，連接
，如圖2.
（Ⅰ）若
、
分別為、
的中點，求證：平面
平面
；
（Ⅱ）求多面體
的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
（
，
）．
（1）若展開式中第5項與第7項的系數之比為3∶8，求k的值；
（2）設
（
），且各項系數
，
，
，…，
互不相同．現把這
個不同系數隨機排成一個三角形數陣：第1列1個數，第2列2個數，…，第n列n個數．設
是第i列中的最小數，其中
，且i，．記
的概率為
．求證：
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程：在平面直角坐標系
中，曲線
：
（
為參數），在以平面直角坐標系的原點為極點、
軸的正半軸為極軸，且與平面直角坐標系取相同單位長度的極坐標系中，曲線
：
.
（1）求曲線的普通方程以及曲線的平面直角坐標方程；
（2）若曲線上恰好存在三個不同的點到曲線的距離相等，求這三個點的極坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用一個平行于底面的截面去截一個正棱錐，截面和底面間的幾何體叫正棱臺.如圖，在四棱臺
中，
，
分別為
的中點.
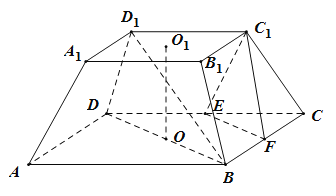
（Ⅰ）求證：
平面
；
（Ⅱ）若側棱所在直線與上下底面中心的連線
所成的角為
，求直線
與平面
所成的角的余弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
