
���}Ŀ��ֱ��![]() �c���タ
�c���タ![]()
![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ����
����![]() ��
��![]() ��
��![]() �S���x�ij˷e��
�S���x�ij˷e��![]() ��
��
��1����![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)�c(di��n)![]() �钁�タ
�钁�タ![]() �Ľ��c(di��n)����(d��ng)
�Ľ��c(di��n)����(d��ng)![]() ��e��С�r(sh��)����ֱ��
��e��С�r(sh��)����ֱ��![]() �ķ��̣�
�ķ��̣�
���𰸡���1��![]() ����2��
����2��![]()
��������
��1���O(sh��)�����c(di��n)������(bi��o)���ɾ��x֮�e��16���ɵ�![]() .���������Ĕ�(sh��)���e����(bi��o)�\(y��n)�㣬��
.���������Ĕ�(sh��)���e����(bi��o)�\(y��n)�㣬��![]() �D(zhu��n)����
�D(zhu��n)����![]() .�����Ã��c(di��n)���ڒ��タ�ϣ��������p��ֵ���Ķ�������タ�ķ��̣�
.�����Ã��c(di��n)���ڒ��タ�ϣ��������p��ֵ���Ķ�������タ�ķ��̣�
��2���O(sh��)��ֱ��l�ķ��̣����뒁�タ���̣����f�_(d��)�����l(f��)�F(xi��n)ֱ��l���^(gu��)���c(di��n)![]() ����
����![]() ��e�Å���(sh��)t��ʾ���������ֵ�����ó��˕r(sh��)��ֱ������.
��e�Å���(sh��)t��ʾ���������ֵ�����ó��˕r(sh��)��ֱ������.
�⣺��1�����}�O(sh��)![]() ��
��![]()
��?y��n)?/span>![]() ��
��![]() ��
��![]() �S�ľ��x�ķe��
�S�ľ��x�ķe��![]() ������
������![]() ��
��
����?y��n)?/span>![]() ��
��![]() ��
��
![]() ��
��![]()
���Ԓ��タ![]() �ķ��̞�
�ķ��̞�![]() ��
��
��2����?y��n)�ֱ��![]() �c���タ�ɂ�(g��)�����c(di��n)������
�c���タ�ɂ�(g��)�����c(di��n)������![]() ��б�ʲ���
��б�ʲ���![]() ��
��
�����O(sh��)![]()
(li��n)��![]() ����
����![]() ��
��
��![]() ��
��![]() ��
��
![]()
��ֱ��![]() ���^(gu��)���c(di��n)
���^(gu��)���c(di��n)![]() ��
��
����![]() ��
��
��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��eȡ����Сֵ
��eȡ����Сֵ![]() ���˕r(sh��)
���˕r(sh��)![]() .
.


 ��1���Ԫ�¿�������ĩϵ�д�
��1���Ԫ�¿�������ĩϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
![]() .
.
��1����![]() ����
����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2��ӑՓ![]() �����c(di��n)��(g��)��(sh��).
�����c(di��n)��(g��)��(sh��).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�
�У�![]() ����Σ�
�����![]() ����
����![]() ��ֱ�ǵĵ���ֱ�������Σ�ƽ��
��ֱ�ǵĵ���ֱ�������Σ�ƽ��![]() ƽ��
ƽ��![]() ��
��
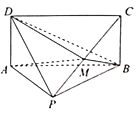
�����C����ƽ��![]() ƽ��
ƽ��![]() ��
��
����![]() ��ֱ��
��ֱ��![]() �����c(di��n)����
�����c(di��n)����![]() ��������
��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���ڡ�����(zh��n)�����ܡ����ҕ��(ji��)Ŀ�ϣ��ס��ҡ�������(g��)�˽M�ɵĽ��܈F(tu��n)�(du��)����һ�(xi��ng)��������(zh��n)���(d��ng)��Ҏ(gu��)�t�����ܴa���ҽo���}Ŀ��Ȼ����![]() ��(g��)�����γ���(ch��ng)���ܣ�ÿ�����r(sh��)�g��
��(g��)�����γ���(ch��ng)���ܣ�ÿ�����r(sh��)�g��![]() ��犃�(n��i)����t����һ��(g��)��.
��犃�(n��i)����t����һ��(g��)��.![]() ��(g��)����ֻҪ��һ�˽������_���t�J(r��n)��ԓ�F(tu��n)�(du��)����(zh��n)�ɹ�����t����(zh��n)ʧ��.����(j��)���������ܜy(c��)ԇ��r����ȡ�˼�
��(g��)����ֻҪ��һ�˽������_���t�J(r��n)��ԓ�F(tu��n)�(du��)����(zh��n)�ɹ�����t����(zh��n)ʧ��.����(j��)���������ܜy(c��)ԇ��r����ȡ�˼�![]() �εĜy(c��)ԇӛ䛣��L�������µ��l�ʷֲ�ֱ���D.
�εĜy(c��)ԇӛ䛣��L�������µ��l�ʷֲ�ֱ���D.
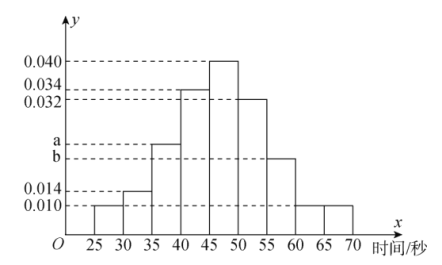
��1�������ܳɹ�����r(sh��)�g����λ��(sh��)��![]() ����
����![]() ��
��![]() ��ֵ�����������
��ֵ�����������![]() ��犃�(n��i)���ܳɹ����l�ʣ�
��犃�(n��i)���ܳɹ����l�ʣ�
��2���ڡ�����(zh��n)�����ܡ���(ji��)Ŀ�����ځ�(l��i)�Ը��������������퉺�����ף��ң������ܳɹ��ĸ��ʷքe��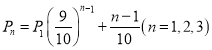 ������
������![]() ��ʾ��
��ʾ��![]() ��(g��)����(ch��ng)�x�ֽ��ܳɹ��ĸ��ʣ�����
��(g��)����(ch��ng)�x�ֽ��ܳɹ��ĸ��ʣ�����![]() ���x��׳���н��ܳɹ����l�ʴ��棬�����Ƿ���ܳɹ����(d��)��.
���x��׳���н��ܳɹ����l�ʴ��棬�����Ƿ���ܳɹ����(d��)��.
����ԓ�F(tu��n)�(du��)����(zh��n)�ɹ��ĸ��ʣ�
��ԓ�F(tu��n)�(du��)��![]() ��С���������żס��ҡ�������(g��)���ψ�(ch��ng)���ܣ���F(tu��n)�(du��)����(zh��n)�ɹ������ɳ����ˆT��(sh��)Ŀ
��С���������żס��ҡ�������(g��)���ψ�(ch��ng)���ܣ���F(tu��n)�(du��)����(zh��n)�ɹ������ɳ����ˆT��(sh��)Ŀ![]() �ķֲ����c��(sh��)�W(xu��)����.
�ķֲ����c��(sh��)�W(xu��)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��������![]() �У�
��![]() ��
��![]() ߅�����c(di��n).
߅�����c(di��n).![]() .
.
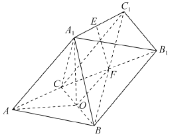
��1���C����![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��
��![]() ��
��![]() ���c(di��n)��
���c(di��n)��![]() ��
��![]() ��
��![]() ���������F
���������F![]() ���w�e.
���w�e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪��������![]() �У���D1����
����D1����![]() ��
��![]() ��
��![]() �龀��
�龀��![]() �����c(di��n)��
�����c(di��n)��![]() ��
��![]() �龀��
�龀��![]() �ϵ��c(di��n)��
�ϵ��c(di��n)��![]() ���F(xi��n)����߅��
���F(xi��n)����߅��![]() ��
��![]() ������D2��
������D2��
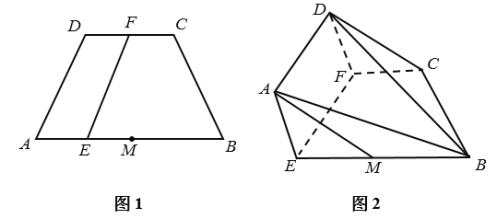
��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2���ڈD2�У���![]() ����ֱ��
����ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵ![]() �У���֪�AC��
�У���֪�AC��![]() ���E�AE��
���E�AE��![]() ��
��![]() ��������c(di��n)A�ڈAC�ϣ��Ҝ�(zh��n)���c�AC����.
��������c(di��n)A�ڈAC�ϣ��Ҝ�(zh��n)���c�AC����.
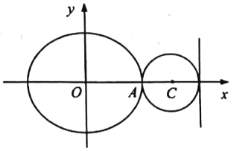
��1����E�AE�ķ��̣�
��2���O(sh��)�^(gu��)�c(di��n)A��ֱ��l�c�AC�ཻ����һ�c(di��n)M���c�E�AE�ཻ����һ�c(di��n)N.��(d��ng)![]() �r(sh��)����ֱ��l�ķ���.
�r(sh��)����ֱ��l�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() �ϵ����ֵ��
�ϵ����ֵ��![]() .
.
��1����a��ֵ��
��2����![]() �څ^(q��)�g
�څ^(q��)�g![]() �ϵ����c(di��n)��(g��)��(sh��).
�ϵ����c(di��n)��(g��)��(sh��).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����Gˮ��ɽ���ǽ�ɽ�yɽ�������B(t��i)�����l(f��)չ�����ѽ�(j��ng)��������,�@���Ƅ�(d��ng)����Դ��܇�a(ch��n)�I(y��)��Ѹ�ٰl(f��)չ���±��ǽ������҇�(gu��)ij�^(q��)����Դ����܇�����N�����c��ݵĽy(t��ng)Ӌ(j��)����
��� | 2014 | 2015 | 2016 | 2017 | 2018 |
�N�����f(w��n)�_(t��i)�� | 8 | 10 | 13 | 25 | 24 |
ij�C(j��)��(g��u)�{(di��o)����ԓ�^(q��)30λُ(g��u)܇܇�����Ԅe�cُ(g��u)܇�N���r���õ��IJ���?j��n)?sh��)��(j��)���±���ʾ��
ُ(g��u)�Â��y(t��ng)ȼ��܇ | ُ(g��u)������Դ܇ | ��Ӌ(j��) | |
����܇�� | 6 | 24 | |
Ů��܇�� | 2 | ||
��Ӌ(j��) | 30 |
��1��������Դ����܇���N��![]() �P(gu��n)�����
�P(gu��n)�����![]() �ľ������P(gu��n)ϵ��(sh��)
�ľ������P(gu��n)ϵ��(sh��)![]() �����Д�
������![]() �c
�c![]() �Ƿ������P(gu��n)��
�Ƿ������P(gu��n)��
��2��Ո(q��ng)������![]() ��(li��n)���a(b��)�����������Д��Ƿ���
��(li��n)���a(b��)�����������Д��Ƿ���![]() �İ����J(r��n)��ُ(g��u)܇܇���Ƿ�ُ(g��u)������Դ����܇�c�Ԅe���P(gu��n)��
�İ����J(r��n)��ُ(g��u)܇܇���Ƿ�ُ(g��u)������Դ����܇�c�Ԅe���P(gu��n)��
������ʽ��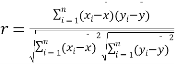 ��
��![]() ������
������![]() .
.![]() ����
����![]() ���t����
���t����![]() �c
�c![]() �������P(gu��n).
�������P(gu��n).
������
| 0��10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com