
【題目】已知函數![]() 是定義在R上的奇函數,當
是定義在R上的奇函數,當![]() 時,
時,![]() ,則下列命題正確的是( )
,則下列命題正確的是( )
A.當![]() 時,
時,![]()
B.函數![]() 有3個零點
有3個零點
C.![]() 的解集為
的解集為![]()
D.![]() ,都有
,都有![]()
【答案】BCD
【解析】
設![]() ,則
,則![]() ,則由題意得
,則由題意得![]() ,根據奇函數
,根據奇函數![]() 即可求出解析式,即可判斷A選項,再根據解析式分類討論即可判斷B、C兩個選項,對函數求導,得單調性,從而求出值域,進而判斷D選項.
即可求出解析式,即可判斷A選項,再根據解析式分類討論即可判斷B、C兩個選項,對函數求導,得單調性,從而求出值域,進而判斷D選項.
解:(1)當![]() 時,
時,![]() ,則由題意得
,則由題意得![]() ,
,
∵ 函數![]() 是奇函數,
是奇函數,
∴ ![]() ,且
,且![]() 時,
時,![]()
![]()
![]() ,A錯;
,A錯;
∴  ,
,
(2)當![]() 時,由
時,由![]() 得
得![]() ,
,
當![]() 時,由
時,由![]() 得
得![]() ,
,
∴ 函數![]() 有3個零點
有3個零點![]() ,B對;
,B對;
(3)當![]() 時,由
時,由![]() 得
得![]() ,
,
當![]() 時,由
時,由![]() 得
得![]() ,
,
∴ ![]() 的解集為
的解集為![]() ,C對;
,C對;
(4)當![]() 時,由
時,由![]() 得
得![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
∴ 函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
∴函數在![]() 上有最小值
上有最小值![]() ,且
,且![]()
![]() ,
,
又∵ 當![]() 時,
時,![]() 時
時![]() ,函數在
,函數在![]() 上只有一個零點,
上只有一個零點,
∴當![]() 時,函數
時,函數![]() 的值域為
的值域為![]() ,
,
由奇函數的圖象關于原點對稱得函數![]() 在
在![]() 的值域為
的值域為![]()
![]() ,
,
∴ 對![]() ,都有
,都有![]() ,D對;
,D對;
故選:BCD.


科目:高中數學 來源: 題型:
【題目】中國古代教育要求學生掌握“六藝”,即“禮、樂、射、御、書、數”.某校為弘揚中國傳統文化,舉行有關“六藝”的知識競賽.甲、乙、丙三位同學進行了決賽.決賽規則:決賽共分![]() 場,每場比賽的第一名、第二名、第三名的得分分別為
場,每場比賽的第一名、第二名、第三名的得分分別為![]() ,選手最后得分為各場得分之和,決賽結果是甲最后得分為
,選手最后得分為各場得分之和,決賽結果是甲最后得分為![]() 分,乙和丙最后得分都為
分,乙和丙最后得分都為![]() 分,且乙在其中一場比賽中獲得第一名,現有下列說法:
分,且乙在其中一場比賽中獲得第一名,現有下列說法:
①每場比賽第一名得分![]() 分;
分;
②甲可能有一場比賽獲得第二名;
③乙有四場比賽獲得第三名;
④丙可能有一場比賽獲得第一名.
則以上說法中正確的序號是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在校園籃球賽中,甲、乙兩個隊10場比賽的得分數據整理成如圖所示的莖葉圖,下列說法正確的是( )
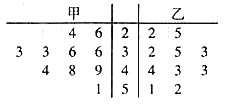
A.乙隊得分的中位數是38.5
B.甲、乙兩隊得分在![]() 分數段頻率相等
分數段頻率相等
C.乙隊的平均得分比甲隊的高
D.甲隊得分的穩定性比乙隊好
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年4月,河北、遼寧、江蘇、福建、湖北、湖南、廣東、重慶等8省市發布高考綜合改革實施方案,決定從2018年秋季入學的高中一年級學生開始實施“![]() ”高考模式.所謂“
”高考模式.所謂“![]() ”,即“3”是指考生必選語文、數學、外語這三科;“1”是指考生在物理、歷史兩科中任選一科;“2”是指考生在生物、化學、思想政治、地理四科中任選兩科.
”,即“3”是指考生必選語文、數學、外語這三科;“1”是指考生在物理、歷史兩科中任選一科;“2”是指考生在生物、化學、思想政治、地理四科中任選兩科.
(1)若某考生按照“![]() ”模式隨機選科,求選出的六科中含有“語文,數學,外語,物理,化學”的概率.
”模式隨機選科,求選出的六科中含有“語文,數學,外語,物理,化學”的概率.
(2)新冠疫情期間,為積極應對“![]() ”新高考改革,某地高一年級積極開展線上教學活動.教育部門為了解線上教學效果,從當地不同層次的學校中抽取高一學生2500名參加語數外的網絡測試,并給前400名頒發榮譽證書,假設該次網絡測試成績服從正態分布,且滿分為450分.
”新高考改革,某地高一年級積極開展線上教學活動.教育部門為了解線上教學效果,從當地不同層次的學校中抽取高一學生2500名參加語數外的網絡測試,并給前400名頒發榮譽證書,假設該次網絡測試成績服從正態分布,且滿分為450分.
①考生甲得知他的成績為270分,考試后不久了解到如下情況:“此次測試平均成績為171分,351分以上共有57人”,請用你所學的統計知識估計甲能否獲得榮譽證書,并說明理由;
②考生丙得知他的實際成績為430分,而考生乙告訴考生丙:“這次測試平均成績為201分,351分以上共有57人”,請結合統計學知識幫助丙同學辨別乙同學信息的真偽,并說明理由.
附:![]() ;
;
![]() ;
;
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古代數學名著《九章算術》中記載:“今有羨除,下廣六尺,上廣一丈,深三尺,末廣八尺,無深,袤七尺,問積幾何?”羨除,即三個面是等腰梯形,兩側面是直角三角形的五面體我們教室打掃衛生用的灰斗近似于一個羨除,又有所不同.如圖所示,ABCD是一個矩形,ABEF和CDFE都是等腰梯形,且平面ABCD⊥平面ABEF,AB=30,BC=10,EF=50,BE=26.則這個灰斗的體積是( )
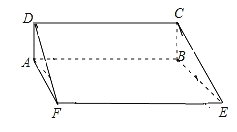
A.3600B.4000C.4400D.4800
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,如圖放置的邊長為2的正方形ABCD沿
中,如圖放置的邊長為2的正方形ABCD沿![]() 軸滾動(無滑動滾動),點D恰好經過坐標原點,設頂點
軸滾動(無滑動滾動),點D恰好經過坐標原點,設頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則對函數
,則對函數![]() 的判斷正確的是( )
的判斷正確的是( )
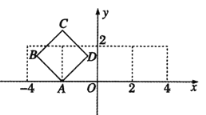
A.函數![]() 在
在![]() 上有兩個零點
上有兩個零點
B.函數![]() 是偶函數
是偶函數
C.函數![]() 在
在![]() 上單調遞增
上單調遞增
D.對任意的![]() ,都有
,都有![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com