）設點C為曲線y＝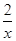
(x>0)上任一點，以點C為圓心的圓與x軸交于點E、A，與y軸交于點E、B.
(1)證明：多邊形EACB的面積是定值，并求這個定值；
(2)設直線y＝－2x＋4與圓C交于點M，N，若|EM|＝|EN|，求圓C的方程．
（1）見解析；（2）(x－2)2＋(y－1)2＝5.
【解析】(1)可直接確定點E為原點，所以設圓心C
，然后根據半徑長度為|OC|，即可寫出圓的標準方程 ,然后再求四邊形的面積看是否是定值即可。
（2）根據圓的幾何性質可知CE所在直線與直線y=-2x+4垂直，所以根據斜率積為-1，即可求出t的值，進而確定圓的方程。
解：(1)證明：設點C (t>0)，因為以點C為圓心的圓與x軸交于點E、A，與y軸交于點E、B.
所以，點E是直角坐標系原點，即E(0,0)．
于是圓C的方程是(x－t)2＋
2＝t2＋
.
則A(2t,0)，B
.
由|CE|＝|CA|＝|CB|知，圓心C在Rt△AEB的斜邊AB上，于是多邊形EACB為Rt△AEB，
其面積S＝
|EA|·|EB|＝×2t×
＝4.
所以多邊形EACB的面積是定值，這個定值是4.
(2)若|EM|＝|EN|，則E在MN的垂直平分線上，即EC是MN的垂直平分線．
因為kEC＝
＝
，kMN＝－2.
所以由kEC·kMN＝－1得t＝2.
所以圓C的方程是(x－2)2＋(y－1)2＝5.
名校課堂系列答案科目：高中數學 來源：2008屆寧夏銀川一中高三年級第四次月考測試、數學試題(理科) 題型：013
設點P是曲線y＝
(－1＜x＜1)上的任意一點，P點處切線的傾斜角為α，則α的取值范圍是
A．[
]
B．(0，
)∪(
，π)
C．[0，]∪[
，π]
D．(，)
查看答案和解析>>
科目：高中數學 來源：吉林省長春外國語學校2011屆高三第一次月考數學試題 題型：013
設點P是曲線y＝x3－
上的任意一點，P點處切線傾斜角為α，則角α的取值范圍是
[0，
)∪[
，π)
[0，
)∪[
，π)
[，π)
(，]
查看答案和解析>>
科目：高中數學 來源：寧夏銀川一中2010屆高三第四次月考、文科數學試卷 題型：044
設點C為曲線y＝
(x＞0)上任一點，以點C為圓心的圓與x軸交于點E、A，與y軸交于點E、B．
(1)證明：多邊形EACB的面積是定值，并求這個定值；
(2)設直線y＝－2x＋4與圓C交于點M，N，若|EM|＝|EN|，求圓C的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
設點P在曲線y＝
ex上，點Q在曲線y＝ln(2x)上，則|PQ
|的最小值為 ( )
A．1－ln2 B.
(1－ln2)
C．1＋ln2 D.(1＋ln2)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com