
設數列 的前n項和為
的前n項和為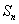 ,數列
,數列 滿足:
滿足: 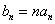 ,且數列
,且數列 的前
的前
n項和為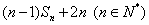 .
.
(1) 求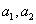 的值;
的值;
(2) 求證:數列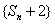 是等比數列;
是等比數列;
(3) 抽去數列 中的第1項,第4項,第7項,……,第3n-2項,……余下的項順序不變,組成一個新數列
中的第1項,第4項,第7項,……,第3n-2項,……余下的項順序不變,組成一個新數列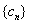 ,若
,若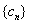 的前n項和為
的前n項和為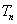 ,求證:
,求證: .
.
解:(1)由題意得: 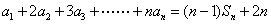 ;………………1分
;………………1分
當n=1時,則有: 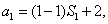 解得:
解得: 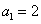 ;
;
當n=2時,則有: 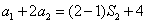 ,即
,即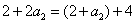 ,解得:
,解得: 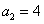 ;
;

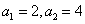 ………………2分
………………2分
(2) 由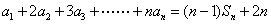 ① 得:
① 得:
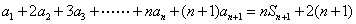 ② ………………3分
② ………………3分
② - ①得: 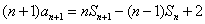 ,
,
即:
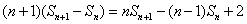 即:
即: ;
……………5分
;
……………5分

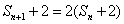 ,由
,由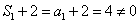 知:
知:
數列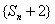 是以4為首項,2為公比的等比數列.…………………………………8分
是以4為首項,2為公比的等比數列.…………………………………8分
(3)由(2)知: 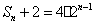 ,即
,即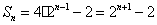 ……………………9分
……………………9分
當n≥2時, 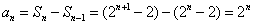 對n=1也成立,
對n=1也成立,
即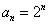 (n
(n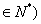 ………………………………………………………….…10分
………………………………………………………….…10分
 數列
數列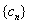 為
為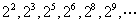 ,它的奇數項組成以4為首項、公比為8的等比數列;偶數項組成以8為首項、公比為8的等比數列;…………………11分
,它的奇數項組成以4為首項、公比為8的等比數列;偶數項組成以8為首項、公比為8的等比數列;…………………11分
 當n=2k-1
當n=2k-1 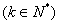 時,
時,
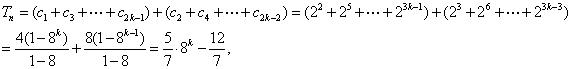
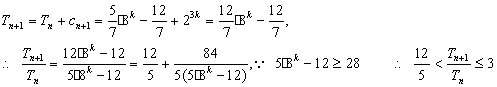 …………………14分
…………………14分
 當n=2k
當n=2k 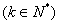 時,
時,
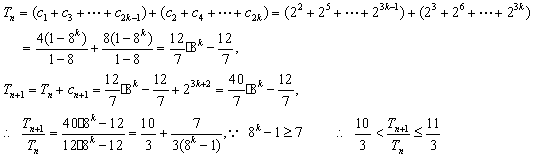

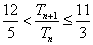 .……………………………………………………………16分
.……………………………………………………………16分


科目:高中數學 來源: 題型:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a4 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2n-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a2n |
| an |
| 4n-1 |
| 2n-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a4 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a22 |
| 1 |
| a2n-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a4 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
| 2011 |
| 2012 |
查看答案和解析>>
科目:高中數學 來源:2011屆廣西省桂林中學高三11月月考數學文卷 題型:解答題
(本小題滿分12分)設數列 的前n項和為Sn=2n2,
的前n項和為Sn=2n2,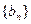 為等比數列,且
為等比數列,且 (Ⅰ)求數列
(Ⅰ)求數列 和
和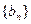 的通項公式;
的通項公式;
(Ⅱ)設 ,求數列
,求數列 的前n項和Tn.
的前n項和Tn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com