
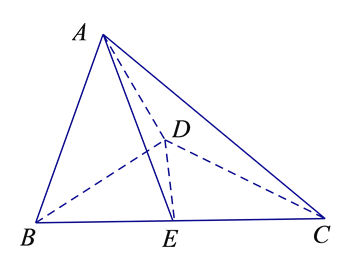
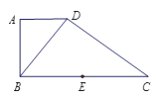
【題目】如圖1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,點E是BC邊的中點,將△ABD沿BD折起,使平面ABD⊥平面BCD,連接AE,AC,DE,得到如圖2所示的幾何體.
(Ⅰ)求證:AB⊥平面ADC;
(Ⅱ)若AD=2,直線CA與平面ABD所成角的正弦值為![]() ,求二面角E-AD-C的余弦值.
,求二面角E-AD-C的余弦值.
【答案】(Ⅰ)見解析; (Ⅱ)![]() .
.
【解析】試題分析:(1)有平面![]() 平面
平面![]() ,證得
,證得![]() ,再根據線面垂直的判定定理,即可作出證明;
,再根據線面垂直的判定定理,即可作出證明;
(Ⅱ)現證得![]() 為直線
為直線![]() 與平面
與平面![]() 所成的角,在
所成的角,在![]() 中,得到
中,得到![]() 的值,即可求解
的值,即可求解![]() ,建立空間直角坐標系
,建立空間直角坐標系![]() ,利用空間向量即可求解二面角的大小.
,利用空間向量即可求解二面角的大小.
試題分析:(Ⅰ)證明:因為平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
又DC⊥BD所以DC⊥平面ABD,所以DC⊥AB,
又AD⊥AB ,所以AB⊥平面ADC
(Ⅱ)因CD⊥平面ABD,所以∠CAD為直線CA與平面ABD所成的角,
CD⊥平面ABD所以CD⊥AD
則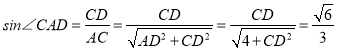
則![]() ,依題意得
,依題意得![]() 所以
所以![]() ,
,
即![]() ,所以
,所以![]()
取BD的中點O,連結AO,EO,因為![]() ,∴AO⊥BD,平面ABD⊥平面BCD,∴AO⊥平面BCD
,∴AO⊥BD,平面ABD⊥平面BCD,∴AO⊥平面BCD
如圖所示建立空間直角坐標系![]() ,
,
則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
由(1)可知AB⊥平面ADC,則平面ADC的法向量![]() ,
,
設平面ADE的法向量![]() ,
, ![]() ,
, ![]() ,
,
則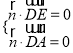 ,即
,即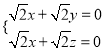 ,令
,令![]() ,得
,得![]() ,
, ![]()
所以![]() ,所以
,所以![]() ,
, ![]() ,由圖可知二面角
,由圖可知二面角![]() 為銳二面角,
為銳二面角,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.


 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源: 題型:
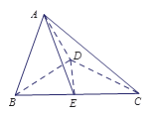
【題目】如圖,在直角梯形![]() 中,
中, ![]() //
// ![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() , 點
, 點![]() 是
是![]() 邊的中點, 將△
邊的中點, 將△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,連接
,連接![]() ,
, ![]() ,
, ![]() , 得到如
, 得到如
圖所示的空間幾何體.
(Ⅰ)求證: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐![]() 的底面為平行四邊形,且
的底面為平行四邊形,且![]() ,
,![]() ,
, ![]() 分別為
分別為![]() 中點,過
中點,過![]() 作平面
作平面![]() 分別與線段
分別與線段![]() 相交于點
相交于點![]() .
.
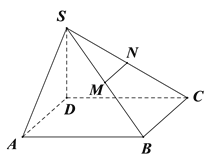
(Ⅰ)在圖中作出平面![]() 使面
使面![]() ‖
‖![]() (不要求證明);
(不要求證明);
(II)若![]() ,在(Ⅰ)的條件下求多面體
,在(Ⅰ)的條件下求多面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究小組在電腦上進行人工降雨模擬實驗,準備用A、B、C三種人工降雨方式分別對甲、乙、丙三地實施人工降雨,其實驗統計結果如下
方式 | 實施地點 | 大雨 | 中雨 | 小雨 | 模擬實驗次數 |
A | 甲 | 2次 | 6次 | 4次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定對甲、乙、丙三地實施的人工降雨彼此互不影響,且不考慮洪澇災害,請根據統計數據:
(1)求甲、乙、丙三地都恰為中雨的概率;
(2)考慮不同地區的干旱程度,當雨量達到理想狀態時,能緩解旱情,若甲、丙地需中雨或大雨即達到理想狀態,乙地必須是大雨才達到理想狀態,記“甲、乙、丙三地中緩解旱情的個數”為隨機變量![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題![]() :
: ![]() ,命題
,命題![]()
![]() .
.
(1)若命題![]() 為真命題,求實數
為真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)若命題![]() 為真命題,求實數
為真命題,求實數![]() 的取值范圍;
的取值范圍;
(3)若命題“![]() ”為真命題,且命題“
”為真命題,且命題“![]() ”為假命題,求實數
”為假命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知⊙![]() :
: ![]() 與⊙
與⊙![]() :
: ![]() ,以
,以![]() ,
, ![]() 分別為左右焦點的橢圓
分別為左右焦點的橢圓![]() :
: ![]() 經過兩圓的交點.
經過兩圓的交點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)![]() ,
, ![]() 分別為橢圓
分別為橢圓![]() 的左右頂點,
的左右頂點, ![]() ,
, ![]() ,
, ![]() 是橢圓
是橢圓![]() 上非頂點的三點,若
上非頂點的三點,若![]() ∥
∥![]() ,
, ![]() ∥
∥![]() ,試問
,試問![]() 的面積是否為定值?若是,求出這個定值;若不是,請說明理由.
的面積是否為定值?若是,求出這個定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中有這樣一則問題:“今有良馬與弩馬發長安,至齊,齊去長安三千里,良馬初日行一百九十三里,日增一十三里;弩馬初日行九十七里,日減半里,良馬先至齊,復還迎弩馬.”則現有如下說法:
①弩馬第九日走了九十三里路;
②良馬前五日共走了一千零九十五里路;
③良馬和弩馬相遇時,良馬走了二十一日.
則以上說法錯誤的個數是( )個
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)設![]() ,求證:數列{bn}是等差數列,并求出{an}的通項公式.
,求證:數列{bn}是等差數列,并求出{an}的通項公式.
(2)設![]() ,數列{cncn+2}的前n項和為Tn,是否存在正整數m,使得
,數列{cncn+2}的前n項和為Tn,是否存在正整數m,使得![]() 對于n∈N*,恒成立?若存在,求出m的最小值;若不存在,請說明.
對于n∈N*,恒成立?若存在,求出m的最小值;若不存在,請說明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com