
【題目】(本小題共13分)已知函數![]()
![]() 的最小正周期為
的最小正周期為![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函數![]() 的單調區間及其圖象的對稱軸方程.
的單調區間及其圖象的對稱軸方程.
【答案】解:(Ⅰ)![]() ………………………2分
………………………2分
![]() , …………………………3分
, …………………………3分
因為![]() 最小正周期為
最小正周期為![]() ,所以
,所以![]() ,解得
,解得![]() ,………………………4分
,………………………4分
所以![]() , …………………… 5分
, …………………… 5分
所以![]() . …………………………6分
. …………………………6分
(Ⅱ)分別由![]() ,
,![]()
可得![]() ,
,![]() ………8分
………8分
所以,函數![]() 的單調增區間為
的單調增區間為![]() ;
;
![]() 的單調減區間為
的單調減區間為![]() ………………………10分
………………………10分
由![]() 得
得![]() .
.
所以,![]() 圖象的對稱軸方程為
圖象的對稱軸方程為![]() . ………………………13分
. ………………………13分
【解析】
試題(Ⅰ)![]()
![]() ,因為
,因為![]() 最小正周期為
最小正周期為![]() ,可得
,可得![]() , 可得
, 可得![]() ,即可求出
,即可求出![]() .(Ⅱ)分別由
.(Ⅱ)分別由![]() ,
,![]() 即可求出單調區間;再根據
即可求出單調區間;再根據![]() ,可得
,可得
![]() 圖象的對稱軸方程.
圖象的對稱軸方程.
試題解析:解:(Ⅰ)![]()
![]() ,
,
因為![]() 最小正周期為
最小正周期為![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以![]() ,
,
所以![]() .
.
(Ⅱ)分別由![]() ,
,![]()
可得![]() ,
,![]()
所以,函數![]() 的單調增區間為
的單調增區間為![]() ;
;
![]() 的單調減區間為
的單調減區間為![]()
由![]() 得
得![]() .
.
所以,![]() 圖象的對稱軸方程為
圖象的對稱軸方程為![]() .
.


科目:高中數學 來源: 題型:
【題目】某商場統計了2008年到2018十一年間某種生活必需品的年銷售額及年銷售額增速圖,其中條形圖表示年(單位:萬元),折線圖年銷售額為年銷售額增長率(%).
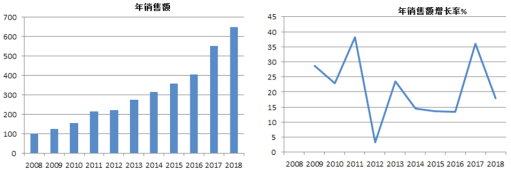
(1)由年銷售額圖判斷,從哪年開始連續三年的年銷售額方差最大?(結論不要求證明)
(2)由年銷售額增長率圖,可以看出2011年銷售額增長率是最高的,能否表示當年銷售額增長最大?(結論不要求證明)
(3)從2010年至2014年這五年中隨機選出兩年,求至少有一年年增長率超過20%的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產的某種產品,如果年返修率不超過千分之一,則其生產部門當年考核優秀,現獲得該公司2011-2018年的相關數據如下表所示:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生產臺數(萬臺) | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
該產品的年利潤(百萬元) | 2.1 | 2.75 | 3.5 | 3.25 | 3 | 4.9 | 6 | 6.5 |
年返修臺數(臺) | 21 | 22 | 28 | 65 | 80 | 65 | 84 | 88 |
部分計算結果:
| ||||||||
注:年返修率=![]()
(1)從該公司2011-2018年的相關數據中任意選取3年的數據,以![]() 表示3年中生產部門獲得考核優秀的次數,求
表示3年中生產部門獲得考核優秀的次數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)根據散點圖發現2015年數據偏差較大,如果去掉該年的數據,試用剩下的數據求出年利潤![]() (百萬元)關于年生產臺數
(百萬元)關于年生產臺數![]() (萬臺)的線性回歸方程(精確到0.01).
(萬臺)的線性回歸方程(精確到0.01).
附:線性回歸方程![]() 中,
中,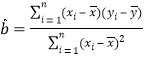
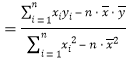 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高一年級學生某次身體素質體能測試的原始成績采用百分制,已知所有這些學生的原始成績均分布在![]() 內,發布成績使用等級制.各等級劃分標準見下表.
內,發布成績使用等級制.各等級劃分標準見下表.
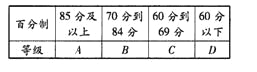
規定:![]() 三級為合格等級,D為不合格等級.為了解該校高一年級學生身體素質情況,從中抽取了
三級為合格等級,D為不合格等級.為了解該校高一年級學生身體素質情況,從中抽取了![]() 名學生的原始成績作為樣本進行統計.按照
名學生的原始成績作為樣本進行統計.按照![]() 的分組作出頻率分布直方圖如圖1所示,樣本中分數在80分及以上的所有數據的莖葉圖如圖2所示.
的分組作出頻率分布直方圖如圖1所示,樣本中分數在80分及以上的所有數據的莖葉圖如圖2所示.
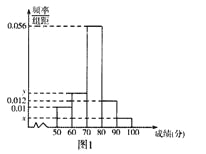
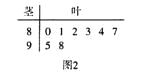
(I)求![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值,并估計該校高一年級學生成績是合格等級的概率;
的值,并估計該校高一年級學生成績是合格等級的概率;
(II)在選取的樣本中,從![]() 兩個等級的學生中隨機抽取2名學生進行調研,求至少有一名學生是
兩個等級的學生中隨機抽取2名學生進行調研,求至少有一名學生是![]() 等級的概率.
等級的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com