【題目】己知函數
，
，
.
（1）討論函數
的單調性；
（2）若
在
處取得極大值，求
的取值范圍.
【答案】(1) 
在
上是遞增的，在
上是遞減的.(2) 
.
【解析】
(1)首先求得導函數的解析式，然后結合函數的定義域分類討論函數的單調性即可；
(2)由題意結合(1)的結論可知
，據此結合導函數的解析式分類討論即可確定實數a的取值范圍.
（1）∵
∴
∵
①當
時，
∴在
上是遞增的
②當
時，若
，則，若
，則
∴在上是遞增的，在上是遞減的.
（2）∵
，∴
由（1）知：
①當
時，
在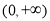上是遞增的，
若
，則
，若
，則
∴
在
取得極小值，不合題意
②
時，在
上是遞增的，在
上是遞減的，
∴
∴在上是遞減的
∴無極值，不合題意.
③當
時，
，由（1）知: 在上是遞增的，
∵
∴若，則，若
，則，
∴在處取得極小值，不合題意.
④當
時，
，由（1）知: 在上是遞減的，
∵
∴若
，則，若），則，
∴在
上是遞增的，在上是遞減的，
故在處取得極大值，符合題意.
綜上所述:.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】某公司為確定下一年度投入某種產品的宣傳費，需了解年宣傳費
（單位：萬元）對年銷售量
（單位：噸）和年利潤
（單位：萬元）的影響．對近六年的年宣傳費
和年銷售量
（
）的數據作了初步統計，得到如下數據：
年份 |
|
|
|
|
|
|
年宣傳費 |
|
|
|
|
|
|
年銷售量 |
|
|
|
|
|
|
經電腦模擬，發現年宣傳費（萬元）與年銷售量（噸）之間近似滿足關系式
（
）．對上述數據作了初步處理，得到相關的值如表：
|
|
|
|
|
|
|
|
（1）根據所給數據，求關于的回歸方程；
（2）已知這種產品的年利潤與，的關系為
若想在
年達到年利潤最大，請預測年的宣傳費用是多少萬元？
附：對于一組數據
，
，…，
，其回歸直線
中的斜率和截距的最小二乘估計分別為
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個口袋內有
個不同的紅球，
個不同的白球，
（1）從中任取個球，紅球的個數不比白球少的取法有多少種？
（2）若取一個紅球記
分，取一個白球記
分，從中任取
個球，使總分不少于
分的取法有多少種？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】求下列函數的解析式：
(1)已知f(x)是二次函數，且f(0)＝2，f(x＋1)－f(x)＝x－1，求f(x)；
(2)已知3f(x)＋2f(－x)＝x＋3，求f(x)．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】公元263年左右，我國數學家劉徽發現，當圓內接多邊形的邊數無限增加時，多邊形面積可無限逼近圓的面積，由此創立了割圓術，利用割圓術劉徽得到了圓周率精確到小數點后面兩位的近似值3.14，這就是著名的徽率．如圖是利用劉徽的割圓術設計的程序框圖，則輸出的n值為 (參考數據：
，
，
)
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某財經頻道報道了某地建筑市場存在違規使用未經淡化海砂的現象．為了研究使用淡化海砂與混凝土耐久性是否達標有關，某大學實驗室隨機抽取了60個樣本，得到了相關數據如下表：
混凝土耐久性達標 | 混凝土耐久性不達標 | 總計 | |
使用淡化海砂 | 25 | t | 30 |
使用未經淡化海砂 | s | 15 | 30 |
總計 | 40 | 20 | 60 |
（Ⅰ）根據表中數據，求出s，t的值，利用獨立性檢驗的方法判斷，能否在犯錯誤的概率不超過1%的前提下認為使用淡化海砂與混凝土耐久性是否達標有關？
（Ⅱ）若用分層抽樣的方法在使用淡化海砂的樣本中抽取了6個，現從這6個樣本中任取2個，則取出的2個樣本混凝土耐久性都達標的概率是多少？
參考數據：
P（K2≥k0） | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
參考公式：
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
