
【題目】設(shè)![]()
(1)證明:當![]() 時,
時,![]() ;
;
(2)當![]() 時
時![]() ,求整數(shù)
,求整數(shù)![]() 的最大值.(參考數(shù)據(jù):
的最大值.(參考數(shù)據(jù):![]() ,
,![]() )
)
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)將![]() 代入函數(shù)解析式可得
代入函數(shù)解析式可得![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,求得
,求得![]() 并令
并令![]() ,由導(dǎo)函數(shù)符號判斷函數(shù)單調(diào)性并求得最大值,由
,由導(dǎo)函數(shù)符號判斷函數(shù)單調(diào)性并求得最大值,由![]() 即可證明
即可證明![]() 恒成立,即不等式得證.
恒成立,即不等式得證.
(2)對函數(shù)求導(dǎo),變形后討論當![]() 時的函數(shù)單調(diào)情況:當
時的函數(shù)單調(diào)情況:當![]() 時,可知滿足題意;將不等式化簡后構(gòu)造函數(shù)
時,可知滿足題意;將不等式化簡后構(gòu)造函數(shù)![]() ,利用導(dǎo)函數(shù)求得極值點與函數(shù)的單調(diào)性,從而求得最小值為
,利用導(dǎo)函數(shù)求得極值點與函數(shù)的單調(diào)性,從而求得最小值為![]() ,分別依次代入檢驗
,分別依次代入檢驗![]() 的符號,即可確定整數(shù)
的符號,即可確定整數(shù)![]() 的最大值;當
的最大值;當![]() 時不滿足題意,因為求整數(shù)
時不滿足題意,因為求整數(shù)![]() 的最大值,所以
的最大值,所以![]() 時無需再討論.
時無需再討論.
(1)證明:當![]() 時代入
時代入![]() 可得
可得![]() ,
,
令![]() ,
,![]() ,
,
則![]() ,
,
令![]() 解得
解得![]() ,
,
當![]() 時
時![]() ,所以
,所以![]() 在
在![]() 單調(diào)遞增,
單調(diào)遞增,
當![]() 時
時![]() ,所以
,所以![]() 在
在![]() 單調(diào)遞減,
單調(diào)遞減,
所以![]() ,
,
則![]() ,即
,即![]() 成立.
成立.
(2)函數(shù)![]()
則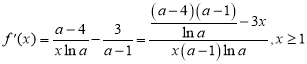 ,
,
若![]() 時,當
時,當![]() 時,
時,![]() ,則
,則![]() 在
在![]() 時單調(diào)遞減,所以
時單調(diào)遞減,所以![]() ,即當
,即當![]() 時
時![]() 成立;
成立;
所以此時需滿足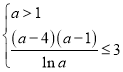 的整數(shù)解即可,
的整數(shù)解即可,
將不等式化簡可得![]() ,
,
令![]()
則![]()
令![]() 解得
解得![]() ,
,
當![]() 時
時![]() ,即
,即![]() 在
在![]() 內(nèi)單調(diào)遞減,
內(nèi)單調(diào)遞減,
當![]() 時
時![]() ,即
,即![]() 在
在![]() 內(nèi)單調(diào)遞增,
內(nèi)單調(diào)遞增,
所以當![]() 時
時![]() 取得最小值,
取得最小值,
則![]() ,
,
![]() ,
,
![]() ,
,
![]()
所以此時滿足![]() 的整數(shù)
的整數(shù)![]() 的最大值為
的最大值為![]() ;
;
當![]() 時,在
時,在![]() 時
時![]() ,此時
,此時![]() ,與題意矛盾,所以不成立.
,與題意矛盾,所以不成立.
因為求整數(shù)![]() 的最大值,所以
的最大值,所以![]() 時無需再討論,
時無需再討論,
綜上所述,當![]() 時
時![]() ,整數(shù)
,整數(shù)![]() 的最大值為
的最大值為![]() .
.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ,
,![]() 是自然對數(shù)的底數(shù))
是自然對數(shù)的底數(shù))
(Ⅰ) 設(shè)![]() (其中
(其中![]() 是
是![]() 的導(dǎo)數(shù)),求
的導(dǎo)數(shù)),求![]() 的極小值;
的極小值;
(Ⅱ) 若對![]() ,都有
,都有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,![]() 平面PCD,
平面PCD,![]() ,
,![]() ,
,![]() ,E為AD的中點,AC與BE相交于點O.
,E為AD的中點,AC與BE相交于點O.

(1)證明:![]() 平面ABCD.
平面ABCD.
(2)求直線BC與平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() ,離心率為
,離心率為![]() ,直線
,直線![]() 恒過
恒過![]() 的一個焦點
的一個焦點![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)設(shè)![]() 為坐標原點,四邊形
為坐標原點,四邊形![]() 的頂點均在
的頂點均在![]() 上,
上,![]() 交于
交于![]() ,且
,且![]() ,若直線
,若直線![]() 的傾斜角的余弦值為
的傾斜角的余弦值為![]() ,求直線
,求直線![]() 與
與![]() 軸交點的坐標.
軸交點的坐標.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
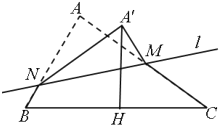
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .過
.過![]() 的中點
的中點![]() 的動直線
的動直線![]() 與線段
與線段![]() 交于點
交于點![]() .將
.將![]() 沿直線
沿直線![]() 向上翻折至
向上翻折至![]() ,使得點
,使得點![]() 在平面
在平面![]() 內(nèi)的投影
內(nèi)的投影![]() 落在線段
落在線段![]() 上.則點
上.則點![]() 的軌跡長度為________.
的軌跡長度為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】百年大計,教育為本.某校積極響應(yīng)教育部號召,不斷加大拔尖人才的培養(yǎng)力度,為清華、北大等排名前十的名校輸送更多的人才.該校成立特長班進行專項培訓(xùn).據(jù)統(tǒng)計有如下表格.(其中![]() 表示通過自主招生獲得降分資格的學(xué)生人數(shù),
表示通過自主招生獲得降分資格的學(xué)生人數(shù),![]() 表示被清華、北大等名校錄取的學(xué)生人數(shù))
表示被清華、北大等名校錄取的學(xué)生人數(shù))
年份(屆) | 2014 | 2015 | 2016 | 2017 | 2018 |
| 41 | 49 | 55 | 57 | 63 |
| 82 | 96 | 108 | 106 | 123 |
(1)通過畫散點圖發(fā)現(xiàn)![]() 與
與![]() 之間具有線性相關(guān)關(guān)系,求
之間具有線性相關(guān)關(guān)系,求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;(保留兩位有效數(shù)字)
的線性回歸方程;(保留兩位有效數(shù)字)
(2)若已知該校2019年通過自主招生獲得降分資格的學(xué)生人數(shù)為61人,預(yù)測2019年高考該校考人名校的人數(shù);
(3)若從2014年和2018年考人名校的學(xué)生中采用分層抽樣的方式抽取出5個人回校宣傳,在選取的5個人中再選取2人進行演講,求進行演講的兩人是2018年畢業(yè)的人數(shù)![]() 的分布列和期望.
的分布列和期望.
參考公式: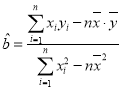 ,
,![]()
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,平面四邊形![]() 中,
中,![]() ,
,![]() 是
是![]() 上的一點,
上的一點,![]() 是
是![]() 的中點,以
的中點,以![]() 為折痕把
為折痕把![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,且
的位置,且![]() .
.
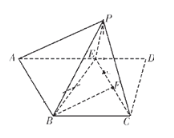
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在多面體ABCDPE中,四邊形ABCD是直角梯形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的余弦值為
的余弦值為![]() ,
,![]() ,F為BE中點,G為PD中點.
,F為BE中點,G為PD中點.
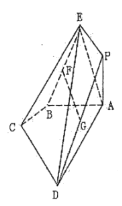
(1)求證:![]() 平面ABCD;
平面ABCD;
(2)求平面BCE與平面ADE所成角(銳角)的余弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com