
【題目】若正項(xiàng)數(shù)列![]() 的首項(xiàng)為
的首項(xiàng)為![]() ,且當(dāng)數(shù)列
,且當(dāng)數(shù)列![]() 是公比為
是公比為![]() 的等比數(shù)列時,則稱數(shù)列
的等比數(shù)列時,則稱數(shù)列![]() 為“
為“![]() 數(shù)列”.
數(shù)列”.
(1)已知數(shù)列![]() 的通項(xiàng)公式為
的通項(xiàng)公式為![]() ,證明:數(shù)列
,證明:數(shù)列![]() 為“
為“![]() 數(shù)列”;
數(shù)列”;
(2)若數(shù)列![]() 為“
為“![]() 數(shù)列”,且對任意
數(shù)列”,且對任意![]() ,
,![]() 、
、![]() 、
、![]() 成等差數(shù)列,公差為
成等差數(shù)列,公差為![]() .
.
①求![]() 與
與![]() 間的關(guān)系;
間的關(guān)系;
②若數(shù)列![]() 為遞增數(shù)列,求
為遞增數(shù)列,求![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)根據(jù)數(shù)列![]() 的通項(xiàng)公式得出
的通項(xiàng)公式得出![]() ,
,![]() ,結(jié)合題中定義可得出結(jié)論;
,結(jié)合題中定義可得出結(jié)論;
(2)①根據(jù)數(shù)列![]() 為“
為“![]() 數(shù)列”,可求得
數(shù)列”,可求得![]() ,再由
,再由![]() 、
、![]() 、
、![]() 成等差數(shù)列可得出
成等差數(shù)列可得出![]() ,由此計算出
,由此計算出![]() ,即可得解;
,即可得解;
②推導(dǎo)出![]() ,利用累加法可分別求出
,利用累加法可分別求出![]() 和
和![]() 的表達(dá)式,根據(jù)數(shù)列
的表達(dá)式,根據(jù)數(shù)列![]() 為遞增數(shù)列可得出
為遞增數(shù)列可得出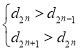 對
對![]() 恒成立,由此可求得
恒成立,由此可求得![]() 的取值范圍.
的取值范圍.
(1)![]() ,
,![]() 且
且![]() ,
,![]() ,
,![]() ,
,
所以,數(shù)列![]() 的首項(xiàng)為
的首項(xiàng)為![]() 且
且![]() 是公比為
是公比為![]() 的等比數(shù)列,故
的等比數(shù)列,故![]() 為“
為“![]() 數(shù)列”;
數(shù)列”;
(2)①![]() 數(shù)列
數(shù)列![]() 為“
為“![]() 數(shù)列”,
數(shù)列”,![]() ,
,![]() ,
,
而![]() 、
、![]() 、
、![]() 成等差數(shù)列,
成等差數(shù)列,![]() ,
,
![]() ;
;
②由①知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以,數(shù)列![]() 的奇數(shù)項(xiàng)與偶數(shù)項(xiàng)分別遞增,
的奇數(shù)項(xiàng)與偶數(shù)項(xiàng)分別遞增,
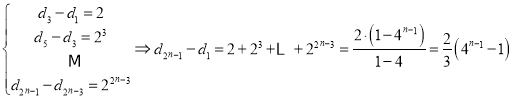 ,
,
![]() ,
,
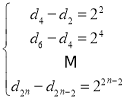 ,
,![]() ,
,
![]() ,
,
因?yàn)椋瑪?shù)列![]() 單調(diào)遞增,
單調(diào)遞增, 對
對![]() 恒成立,
恒成立,
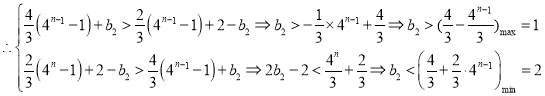 ,
,
故![]() 的取值范圍為
的取值范圍為![]() .
.


 智能訓(xùn)練練測考系列答案
智能訓(xùn)練練測考系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(題文)已知橢圓![]() 的離心率為
的離心率為![]() ,過點(diǎn)
,過點(diǎn)![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 與
與![]() 兩點(diǎn),
兩點(diǎn),![]() ,且當(dāng)直線
,且當(dāng)直線![]() 垂直于
垂直于![]() 軸時,
軸時,![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() ,求弦長
,求弦長![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年9月25日.阿里巴巴在杭州云棲大會上正式對外發(fā)布了含光800AI芯片,在業(yè)界標(biāo)準(zhǔn)的ResNet -50測試中,含光800推理性能達(dá)到78563lPS,比目前業(yè)界最好的AI芯片性能高4倍;能效比500 IPS/W,是第二名的3.3倍.在國內(nèi)集成電路產(chǎn)業(yè)發(fā)展中,集成電路設(shè)計產(chǎn)業(yè)始終是國內(nèi)集成電路產(chǎn)業(yè)中最具發(fā)展活力的領(lǐng)域,增長也最為迅速.如圖是2014-2018年中國集成電路設(shè)計產(chǎn)業(yè)的銷售額(億元)及其增速(%)的統(tǒng)計圖,則下面結(jié)論中正確的是( )
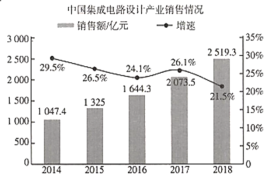
A.2014-2018年,中國集成電路設(shè)計產(chǎn)業(yè)的銷售額逐年增加
B.2014-2017年,中國集成電路設(shè)計產(chǎn)業(yè)的銷售額增速逐年下降
C.2018年中國集成電路設(shè)計產(chǎn)業(yè)的銷售額的增長率比2015年的高
D.2018年與2014年相比,中國集成電路設(shè)計產(chǎn)業(yè)銷售額的增長率約為110%
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知長方形ABCD中,AB=1,∠ABD=60°,現(xiàn)將長方形ABCD沿著對角線BD折起,使平面ABD⊥平面BCD,則折后幾何圖形的外接球表面積為_____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,以坐標(biāo)原點(diǎn)O為極點(diǎn),以x軸正半軸為極軸,建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為![]() 射線
射線![]() 交曲線C于點(diǎn)A,傾斜角為α的直線l過線段OA的中點(diǎn)B且與曲線C交于P、Q兩點(diǎn).
交曲線C于點(diǎn)A,傾斜角為α的直線l過線段OA的中點(diǎn)B且與曲線C交于P、Q兩點(diǎn).
(1)求曲線C的直角坐標(biāo)方程及直線l的參數(shù)方程;
(2)當(dāng)直線l傾斜角α為何值時, |BP|·|BQ|取最小值, 并求出|BP|·|BQ|最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)舉行的“新冠肺炎”防控知識閉卷考試比賽,總分獲得一等獎、二等獎、三等獎的代表隊(duì)人數(shù)情況如下表,該校政教處為使頒獎儀式有序進(jìn)行,氣氛活躍,在頒獎過程中穿插抽獎活動,并用分層抽樣的方法從三個代表隊(duì)中共抽取16人在前排就坐,其中一等獎代表隊(duì)有6人.
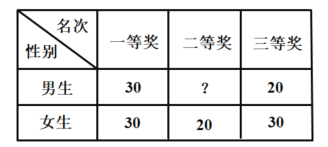
(1)求二等獎代表隊(duì)的男生人數(shù);
(2)從前排就坐的三等獎代表隊(duì)員5人(2男3女)中隨機(jī)抽取3人上臺領(lǐng)獎,請求出只有一個男生上臺領(lǐng)獎的概率;
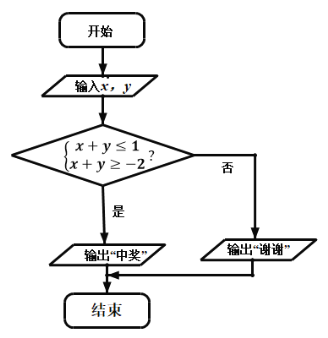
(3)抽獎活動中,代表隊(duì)員通過操作按鍵,使電腦自動產(chǎn)生[![]() 2,2]內(nèi)的兩個均勻隨機(jī)數(shù)x,y,隨后電腦自動運(yùn)行如圖所示的程序框圖的相應(yīng)程序,若電腦顯示“中獎”,則代表隊(duì)員獲相應(yīng)獎品;若電腦顯示“謝謝”,則不中獎,求代表隊(duì)隊(duì)員獲得獎品的概率.
2,2]內(nèi)的兩個均勻隨機(jī)數(shù)x,y,隨后電腦自動運(yùn)行如圖所示的程序框圖的相應(yīng)程序,若電腦顯示“中獎”,則代表隊(duì)員獲相應(yīng)獎品;若電腦顯示“謝謝”,則不中獎,求代表隊(duì)隊(duì)員獲得獎品的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,四邊形ABCD為等腰梯形,AB=4,AD=DC=CB=2,△ADC沿AC折起,使得平面ADC⊥平面ABC,E為AB的中點(diǎn),連接DE,DB(如圖2).
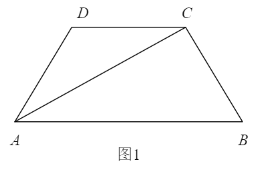
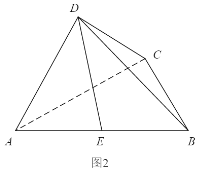
(1)求證:BC⊥AD
(2)求直線DE與平面BCD所成的角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“珠算之父”程大位是我國明代著名的數(shù)學(xué)家,他的應(yīng)用巨著《算法統(tǒng)綜》中有一首“竹筒容米”問題:“家有九節(jié)竹一莖,為因盛米不均平,下頭三節(jié)四升五,上梢四節(jié)三升八,唯有中間兩節(jié)竹,要將米數(shù)次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容積依次相差同一數(shù)量.)用你所學(xué)的數(shù)學(xué)知識求得中間兩節(jié)竹的容積為
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,拋物線
,拋物線![]() 上的點(diǎn)到準(zhǔn)線的最小距離為
上的點(diǎn)到準(zhǔn)線的最小距離為![]() .
.
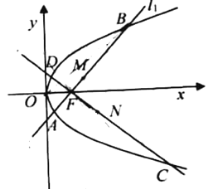
(1)求拋物線![]() 的方程;
的方程;
(2)若過點(diǎn)![]() 作互相垂直的兩條直線
作互相垂直的兩條直線![]() 、
、![]() ,
,![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點(diǎn),
兩點(diǎn),![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點(diǎn),
兩點(diǎn),![]() 分別為弦
分別為弦![]() 的中點(diǎn),求
的中點(diǎn),求![]() 的最小值.
的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com