
【題目】已知橢圓![]() 的長軸長為
的長軸長為![]() ,且離心率為
,且離心率為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)橢圓![]() 的左焦點為
的左焦點為![]() ,點
,點![]() 是橢圓與
是橢圓與![]() 軸負(fù)半軸的交點,經(jīng)過
軸負(fù)半軸的交點,經(jīng)過![]() 的直線
的直線![]() 與橢圓交于點
與橢圓交于點![]() ,經(jīng)過
,經(jīng)過![]() 且與
且與![]() 平行的直線與橢圓交于點
平行的直線與橢圓交于點![]() ,若
,若![]() ,求直線
,求直線![]() 的方程.
的方程.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國在北宋年間(公元1084年)第一次印刷出版了《算經(jīng)十書》,即賈憲的《黃帝九章算法細(xì)草》,劉益的《議古根源》,秦九韶的《數(shù)書九章》,李冶的《測圓海鏡》和《益古演段》,楊輝的《詳解九章算法》、《日用算法》和《楊輝算法》,朱世杰的《算學(xué)啟蒙》和《四元玉鑒》.這些書中涉及的很多方面都達(dá)到古代數(shù)學(xué)的高峰,其中一些“算法”如開立方和開四次方也是當(dāng)時世界數(shù)學(xué)的高峰.哈三中圖書館中正好有這十本書,現(xiàn)在小張同學(xué)從這十本書中任借三本閱讀,那么他借到的三本書中書名中恰有一個“算”字的概率為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() .
.
(1)當(dāng)![]() 時,若對任意
時,若對任意![]() 均有
均有![]() 成立,求實數(shù)k的取值范圍;
成立,求實數(shù)k的取值范圍;
(2)設(shè)直線![]() 與曲線
與曲線![]() 和曲線
和曲線![]() 均相切,切點分別為
均相切,切點分別為![]() ,
,![]() ,其中
,其中![]() .
.
①求證:![]() ;
;
②當(dāng)![]() 時,關(guān)于x的不等式
時,關(guān)于x的不等式![]() 恒成立,求實數(shù)a的取值范圍.
恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知某市穿城公路![]() 自西向東到達(dá)市中心
自西向東到達(dá)市中心![]() 后轉(zhuǎn)向東北方向,
后轉(zhuǎn)向東北方向,![]() ,現(xiàn)準(zhǔn)備修建一條直線型高架公路
,現(xiàn)準(zhǔn)備修建一條直線型高架公路![]() ,在
,在![]() 上設(shè)一出入口
上設(shè)一出入口![]() ,在
,在![]() 上設(shè)一出入口
上設(shè)一出入口![]() ,且要求市中心
,且要求市中心![]() 到
到![]() 所在的直線距離為
所在的直線距離為![]() .
.
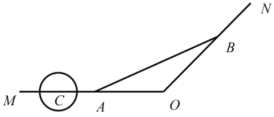
(1)求![]() ,
,![]() 兩出入口間距離的最小值;
兩出入口間距離的最小值;
(2)在公路![]() 段上距離市中心
段上距離市中心![]() 點
點![]() 處有一古建筑
處有一古建筑![]() (視為一點),現(xiàn)設(shè)立一個以
(視為一點),現(xiàn)設(shè)立一個以![]() 為圓心,
為圓心,![]() 為半徑的圓形保護(hù)區(qū),問如何在古建筑
為半徑的圓形保護(hù)區(qū),問如何在古建筑![]() 和市中心
和市中心![]() 之間設(shè)計出入口
之間設(shè)計出入口![]() ,才能使高架公路及其延長線不經(jīng)過保護(hù)區(qū)?
,才能使高架公路及其延長線不經(jīng)過保護(hù)區(qū)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=Asin(x+)(A>0,>0,0<<)的部分圖象如圖所示,又函數(shù)g(x)=f(x+![]() ).
).
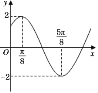
(1)求函數(shù)g(x)的單調(diào)增區(qū)間;
(2)設(shè)![]() ABC的內(nèi)角ABC的對邊分別為abc,又c=
ABC的內(nèi)角ABC的對邊分別為abc,又c=![]() ,且銳角C滿足g(C)= -1,若sinB=2sinA,,求ABC的面積.
,且銳角C滿足g(C)= -1,若sinB=2sinA,,求ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,點E在
,點E在![]() 上,且
上,且![]() ,將三角形
,將三角形![]() 沿線段
沿線段![]() 折起到
折起到![]() 的位置,
的位置,![]() (如圖2).
(如圖2).
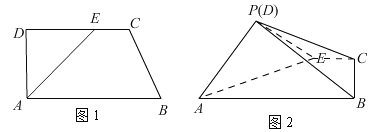
(1)求證:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點M,使
上是否存在點M,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() ,
,![]() ,動圓
,動圓![]() 與圓
與圓![]() 、
、![]() 都相切,則動圓
都相切,則動圓![]() 的圓心軌跡
的圓心軌跡![]() 的方程為________;直線
的方程為________;直線![]() 與曲線
與曲線![]() 僅有三個公共點,依次為
僅有三個公共點,依次為![]() 、
、![]() 、
、![]() ,則
,則![]() 的最大值為________.
的最大值為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范圍;
的取值范圍;
(3)當(dāng)![]() 時,設(shè)
時,設(shè)![]() ,求
,求![]() 在區(qū)間
在區(qū)間![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,橢圓![]() 的右頂點為
的右頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,過點
,過點![]()
且斜率為![]() 的直線與
的直線與![]() 軸交于點
軸交于點![]() , 與橢圓交于另一個點
, 與橢圓交于另一個點![]() ,且點
,且點![]() 在
在![]() 軸上的射影恰好為點
軸上的射影恰好為點![]() .
.
(Ⅰ)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(Ⅱ)過點![]() 且斜率大于
且斜率大于![]() 的直線與橢圓交于
的直線與橢圓交于![]() 兩點(
兩點(![]() ),若
),若![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com