
(本題11分)如圖1,拋物線y=ax2+bx+c(a≠0)的頂點為(1,4),交x軸于A、B,交y軸于D,其中B點的坐標為(3,0)
(1)求拋物線的解析式
(2)如圖 2,過點A的直線與拋物線交于點E,交y軸于點F,其中E點的橫坐標為2,若直線PQ為拋物線的對稱軸,點G為PQ上一動點,則
2,過點A的直線與拋物線交于點E,交y軸于點F,其中E點的橫坐標為2,若直線PQ為拋物線的對稱軸,點G為PQ上一動點,則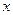 軸上是否存在一點H,使D、G、F、H四點圍成的四邊形周長最小.若存在,求出這個最小值及G、H的坐
軸上是否存在一點H,使D、G、F、H四點圍成的四邊形周長最小.若存在,求出這個最小值及G、H的坐 標;若不存在,請說明理由.
標;若不存在,請說明理由.
(3)如圖3,拋物線上是否存在一點 ,過點
,過點 作
作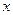 軸的垂線,垂足為
軸的垂線,垂足為 ,過點
,過點 作直線
作直線 ,交線段
,交線段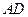 于點
于點 ,連接
,連接 ,使
,使 ~
~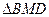 ,若存在,求出點
,若存在,求出點 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.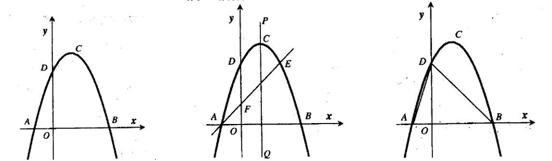 圖1 圖2
圖1 圖2  圖3
圖3
解:(1 )設所求拋物線的解析式為:
)設所求拋物線的解析式為: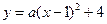 ,依題意,將點B(3,0)代入,得
,依題意,將點B(3,0)代入,得 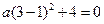 解得:a=-1 ∴所求拋物線的解析式為:
解得:a=-1 ∴所求拋物線的解析式為: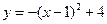
(2)如圖6,在y軸的負半軸上取一點I,使得點F與點I關于x軸對稱,
在x軸上取一點H,連接HF、HI、HG、GD、GE,則HF=HI…………………①
設過A、E兩點的一次函數解析式為:y=kx+b(k≠0),
∵點E在拋物線上且點E的橫坐標為2,將x=2代入拋物線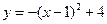 ,得
,得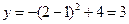
∴點E坐標為(2,3)
又∵拋物線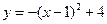 圖像分別與x軸、y軸交于點A、B、D
圖像分別與x軸、y軸交于點A、B、D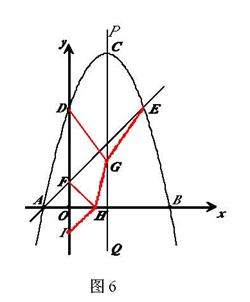
∴當y=0時,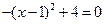 ,∴x=-1或x=3
,∴x=-1或x=3
當x=0時,y=-1+4=3,
∴點A(-1,0),點B(3,0),點D(0,3) 
又∵拋物線的對稱軸為:直線x=1,
∴點D與點E關于PQ對稱,GD=GE…………………②
分別將點A(-1,0)、點E(2,3)代入y=kx+b,得: 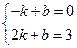
解得: 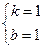
過A、E兩點的一次函數解析式為:y=x+1
∴當x=0 時,y=1
時,y=1
∴點F坐標為(0,1)
∴ =2………………………………………③
=2………………………………………③
又∵點F與點I關于x軸 對稱,
對稱,
∴點I坐標為(0,-1)
∴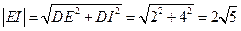 ………④
………④
又∵要使四邊形DFHG的周長最小,由于DF是一個定值,
∴只要使 DG+GH+HI最小即可
DG+GH+HI最小即可
由圖形的對稱性和①、②、③,可知,
DG+GH+HF=EG+GH+HI
只有當EI為一條直線時,EG+GH+HI最小
設過E(2,3)、I(0,-1)兩點的函數解析式為: ,
,
分別將點E(2,3)、點I(0,-1)代入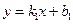 ,得:
,得: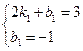
解得: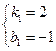
過I、E兩點的一次函數解析式為:y=2x-1
∴當x=1時,y=1;當y=0時,x=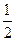 ;
;
∴點G坐標為(1,1),點H坐標為(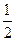 ,0)
,0)
∴四邊形DFHG的周長最小為:DF+DG+GH+HF=DF+EI
由③和④,可知:
DF+EI=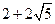
∴四邊形DFHG的周長最小為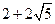 。
。
(3)如圖7,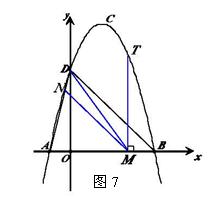
由 題意可知,∠NMD=∠MDB,
題意可知,∠NMD=∠MDB,
要使,△DNM∽△BMD,只要使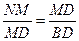 即可,
即可,
即: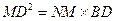 ………………………………⑤
………………………………⑤
設點M的坐標為(a,0),由MN∥BD,可得
△AMN∽△ABD,
∴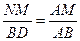
再由(1)、(2)可知,AM=1+a,BD=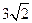 ,AB=4
,AB=4
∴ 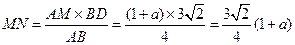
∵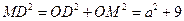 ,
,
∴⑤式可寫成: 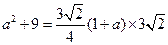
解得 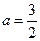 或
或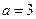 (不合題意,舍去)∴點M的坐標為(
(不合題意,舍去)∴點M的坐標為(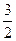 ,0)
,0)
又∵點T在拋物線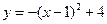 圖像上,
圖像上,
∴當x=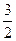 時,y=
時,y=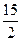
 ∴點T的坐標為(
∴點T的坐標為(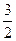 ,
,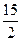 ).
).
解析


科目:高中數學 來源: 題型:解答題
設雙曲線C: -y2=1的左、右頂點分別為A1、A2,垂直于x軸的直線m與雙曲線C交于不同的兩點P、Q.
-y2=1的左、右頂點分別為A1、A2,垂直于x軸的直線m與雙曲線C交于不同的兩點P、Q.
(1)若直線m與x軸正半軸的交點為T,且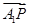 ·
·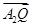 =1,求點T的坐標;
=1,求點T的坐標;
(2)求直線A1P與直線A2Q的交點M的軌跡E的方程;
(3)過點F(1,0)作直線l與(2)中的軌跡E交于不同的兩點A、B,設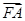 =λ·
=λ·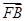 ,若λ∈[-2,-1],求|
,若λ∈[-2,-1],求|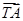 +
+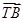 |(T為(1)中的點)的取值范圍.
|(T為(1)中的點)的取值范圍.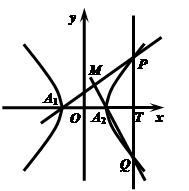
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(12分) 在直角坐標系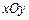 中,點
中,點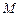 到點
到點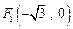 ,
, 的距離之和是
的距離之和是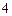 ,點
,點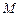 的軌跡是
的軌跡是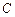 ,直線
,直線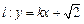 與軌跡
與軌跡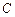 交于不同的兩點
交于不同的兩點 和
和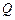 .⑴求軌跡
.⑴求軌跡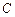 的方程;⑵是否存在常數
的方程;⑵是否存在常數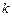 ,
,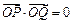 ?若存在,求出
?若存在,求出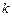 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)已知橢圓的中心在原點,焦點在y軸上,離心率為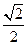 ,且
,且
橢圓經過圓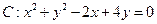 的圓心C。
的圓心C。
(I)求橢圓的標準方程;
(II)設直線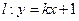 與橢圓交于A、B兩點,點
與橢圓交于A、B兩點,點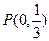 且|PA|=|PB|,求直線
且|PA|=|PB|,求直線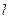 的方程。
的方程。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知一隧道的截面 是一個半橢圓面(如圖所示),要保證車輛正常通行,車頂離隧道頂部至少要有
是一個半橢圓面(如圖所示),要保證車輛正常通行,車頂離隧道頂部至少要有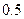 米的距離,現有一貨車,車寬
米的距離,現有一貨車,車寬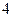 米,車高
米,車高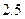 米.
米.
(1)若此隧道為單向通行,經測量隧道的跨度是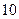 米,則應如何設計隧道才能保證此貨車正常通行?
米,則應如何設計隧道才能保證此貨車正常通行?
(2)圓可以看作是長軸短軸相等的特殊橢圓,類比圓面積公式,
請你推測橢圓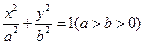 的面積公式.并問,當隧道為雙向通行(車道間的距離忽略不記)時,要使此貨車安全通過,應如何設計隧道,才會使同等隧道長度下開鑿的土方量最小?
的面積公式.并問,當隧道為雙向通行(車道間的距離忽略不記)時,要使此貨車安全通過,應如何設計隧道,才會使同等隧道長度下開鑿的土方量最小?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com