
如圖,三棱錐 中,側面
中,側面 底面
底面 ,
,  ,且
,且 ,
, .(Ⅰ)求證:
.(Ⅰ)求證: 平面
平面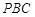 ;
;
(Ⅱ)若 為側棱PB的中點,求直線AE與底面
為側棱PB的中點,求直線AE與底面 所成角的正弦值.
所成角的正弦值.

【解析】第一問中,利用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以 第二問中結合取AC中點O,連接PO、OB,并取OB中點H,連接AH、EH,因為PA=PC,所以PO⊥AC,同(Ⅰ)易證
第二問中結合取AC中點O,連接PO、OB,并取OB中點H,連接AH、EH,因為PA=PC,所以PO⊥AC,同(Ⅰ)易證 平面ABC,又EH//PO,所以EH平面
平面ABC,又EH//PO,所以EH平面 ABC ,
ABC ,
則 為直線AE與底面ABC 所成角,
為直線AE與底面ABC 所成角,

解
(Ⅰ) 證明:由用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以
………………………………………………6分
(Ⅱ)如圖, 取AC中點O,連接PO、OB,并取OB中點H,連接AH、EH,
因為PA=PC,所以PO⊥AC,同(Ⅰ)易證 平面ABC,
平面ABC,
又EH//PO,所以EH平面 ABC ,
ABC ,
則 為直線AE與底面ABC 所成角,
為直線AE與底面ABC 所成角,
且 ………………………………………10分
………………………………………10分
又PO=1/2AC= ,也所以有EH=1/2PO=
,也所以有EH=1/2PO= ,
,
由(Ⅰ)已證 平面PBC,所以
平面PBC,所以 ,即
,即 ,
,
故 ,
,
于是
所以直線AE與底面ABC 所成角的正弦值為

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
 (2012•湖南模擬)如圖,三棱錐P-ABC中,側面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模擬)如圖,三棱錐P-ABC中,側面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2| 2 |
查看答案和解析>>
科目:高中數學 來源:2013-2014學年黑龍江哈師大附中高三上期期中考試理科數學試卷(解析版) 題型:解答題
如圖,在三棱錐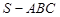 中,側面
中,側面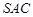 與底面
與底面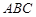 垂直,
垂直, 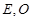 分別是
分別是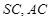 的中點,
的中點,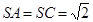 ,
,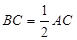 ,
,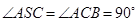 .
.
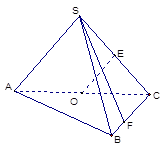
(1)若點 在線段
在線段 上,問:無論
上,問:無論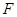 在
在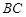 的何處,是否都有
的何處,是否都有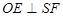 ?請證明你的結論;
?請證明你的結論;
(2)求二面角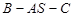 的平面角的余弦.
的平面角的余弦.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年黑龍江哈師大附中高三上期期中考試文科數學試卷(解析版) 題型:解答題
如圖,在三棱錐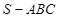 中,側面
中,側面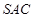 與底面
與底面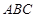 垂直,
垂直, 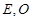 分別是
分別是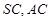 的中點,
的中點, 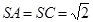 ,
,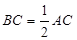 ,
, .
.
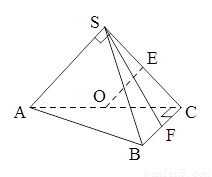
(Ⅰ)求證: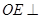 平面
平面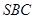 ;
;
(Ⅱ)若點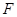 為線段
為線段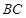 的中點,求異面直線
的中點,求異面直線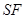 與
與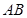 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省韶關市高三第一次調研測試數學理科試卷(解析版) 題型:解答題
如圖,三棱錐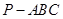 中,
中,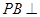 底面
底面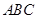 于
于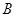 ,
,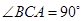 ,
,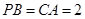 ,點
,點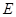 是
是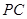 的中點.
的中點.

(1)求證:側面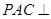 平面
平面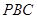 ;
;
(2)若異面直線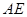 與
與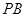 所成的角為
所成的角為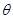 ,且
,且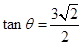 ,
,
求二面角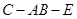 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年河南鄭州盛同學校高三4月模擬考試文科數學試卷(解析版) 題型:解答題
如圖,三棱錐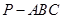 中,
中,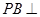 底面ABC于B,
底面ABC于B,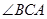 =900,
=900,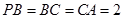 ,點E、F分別是PC、AP的中點。
,點E、F分別是PC、AP的中點。

(1)求證:側面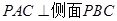 ;
;
(2)求異面直線AE與BF所成的角;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com