【題目】已知函數
在區間
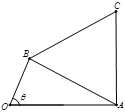
上單調遞增,在區間
上單調遞減;如圖,四邊形
中,
,
,
為
的內角
的對邊，
且滿足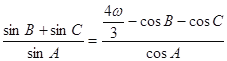
.
（Ⅰ）證明：
；
（Ⅱ）若
，設
，
,
，求四邊形面積的最大值.
【答案】(1)正弦定理的運用根據邊角的轉換來得到證明。
(2)
時取最大值,
的最大值為
【解析】
試題分析：（1）利用兩角和正弦公式和降冪公式化簡，要熟練掌握公式，不要把符號搞錯，很多同學化簡不正確，求解較復雜三角函數的最值時，首先化成
形式，在求最大值或最小值,尋求角與角之間的關系，化非特殊角為特殊角，靈活的掌握兩角和的正弦公式進行化簡；（2）在三角形中，處理三角形的邊角關系時，一般全部化成角的關系，或全部化成邊的關系，解決三角形問題時，注意角的范圍；（3）把形如
化為
，可進一步研究函數的周期、單調性、最值和對稱性.
試題解析：解:（1）由題意知:
,解得:
,
（2）因為
,所以
,所以
為等邊三角形
,
,
,
當且僅當
即時取最大值,
的最大值為.
科目：高中數學 來源： 題型：
【題目】某校參加夏令營的同學有3名男同學
和3名女同學
，其所屬年級情況如下表：
高一年級 | 高二年級 | 高三三年級 | |
男同學 |
|
|
|
女同學 |
|
|
|
現從這6名同學中隨機選出2人參加知識競賽（每人被選到的可能性相同）
（1）用表中字母寫出這個試驗的樣本空間；
（2）設
為事件“選出的2人來自不同年級且恰有1名男同學和1名女同學”，寫出事件的樣本點，并求事件發生的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）的定義域為（0，＋∞），且滿足f（2）＝1，f（xy）＝f（x）＋f（y），又當x2>x1>0時，f（x2）>f（x1）．
（1）求f（1）、f（4）、f（8）的值；
（2）若有f（x）＋f（x－2）≤3成立，求x的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某理財公司有兩種理財產品A和B，這兩種理財產品一年后盈虧的情況如下（每種理財產品的不同投資結果之間相互獨立）：
產品A
投資結果 | 獲利40% | 不賠不賺 | 虧損20% |
概率 |
|
|
|
產品B
投資結果 | 獲利20% | 不賠不賺 | 虧損10% |
概率 | p |
| q |
注：p＞0，q＞0
（1）已知甲、乙兩人分別選擇了產品A和產品B投資，如果一年后他們中至少有一人獲利的概率大于
，求實數p的取值范圍；
（2）若丙要將家中閑置的10萬元人民幣進行投資，以一年后投資收益的期望值為決策依據，則選用哪種產品投資較理想？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓心為
的圓過原點
，且直線
與圓相切于點
.
（1）求圓的方程；
（2）已知過點
的直線
的斜率為
，且直線與圓相交于
兩點.
①若
，求弦
的長；
②若圓上存在點
，使得
成立，求直線的斜率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（1）若
，求函數
的極小值；
（2）設函數
，試問：在定義域內是否存在三個不同的自變量
使得
的值相等，若存在，請求出
的范圍，若不存在，請說明理由？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
