
【題目】如圖,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,點(diǎn)E,F分別在
,點(diǎn)E,F分別在![]() ,
,![]() ,且
,且![]() ,
,![]() .設(shè)
.設(shè)![]() .
.
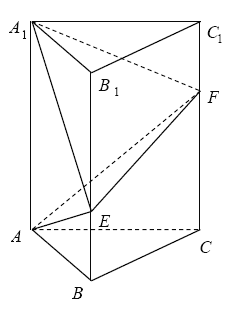
(1)當(dāng)![]() 時(shí),求異面直線
時(shí),求異面直線![]() 與
與![]() 所成角的大小;
所成角的大小;
(2)當(dāng)平面![]() 平面
平面![]() 時(shí),求
時(shí),求![]() 的值.
的值.
【答案】(1)60°(2)![]()
【解析】
(1)推導(dǎo)出![]() 平面ABC,
平面ABC,![]() AC,建立分別以AB,AC,
AC,建立分別以AB,AC,![]() 為
為![]() 軸的空間直角坐標(biāo)系,利用法向量能求出異面直線AE與
軸的空間直角坐標(biāo)系,利用法向量能求出異面直線AE與![]() 所成角.
所成角.
(2)推導(dǎo)出平面![]() 的法向量和平面
的法向量和平面![]() 的一個(gè)法向量,由平面
的一個(gè)法向量,由平面![]() 平面
平面![]() ,能求出
,能求出![]() 的值.
的值.
解:因?yàn)橹比庵?/span>![]() ,
,
所以![]() 平面
平面![]() ,
,
因?yàn)?/span>![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
又因?yàn)?/span>![]() ,
,
所以建立分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸的空間直角坐標(biāo)系
軸的空間直角坐標(biāo)系![]() .
.
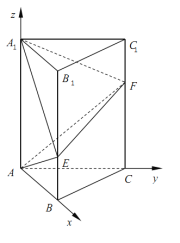
(1)設(shè)![]() ,則
,則![]() ,
,![]() ,
,
各點(diǎn)的坐標(biāo)為![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
因?yàn)?/span>![]() ,
,![]() ,
,
所以 .
.
所以向量![]() 和
和![]() 所成的角為120°,
所成的角為120°,
所以異面直線![]() 與
與![]() 所成角為60°;
所成角為60°;
(2)因?yàn)?/span>![]() ,
,![]() ,
,
![]() ,
,![]()
設(shè)平面![]() 的法向量為
的法向量為![]() ,
,
則![]() ,且
,且![]() .
.
即![]() ,且
,且![]() .
.
令![]() ,則
,則![]() ,
,![]() .
.
所以![]() 是平面
是平面![]() 的一個(gè)法向量.
的一個(gè)法向量.
同理,![]() 是平面
是平面![]() 的一個(gè)法向量.
的一個(gè)法向量.
因?yàn)槠矫?/span>![]() 平面
平面![]() ,
,
所以![]() ,
,
![]() ,
,
解得![]() .
.
所以當(dāng)平面![]() 平面
平面![]() 時(shí),
時(shí),![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】新能源汽車是我國汽車工業(yè)由大變強(qiáng)的一條必經(jīng)之路!國家對(duì)其給予政策上的扶持,己成為我國的戰(zhàn)略方針.近年來,我國新能源汽車制造蓬勃發(fā)展,某著名車企自主創(chuàng)新,研發(fā)了一款新能源汽車,經(jīng)過大數(shù)據(jù)分析獲得:在某種路面上,該品牌汽車的剎車距離![]() (米)與其車速
(米)與其車速![]() (千米/小時(shí))滿足下列關(guān)系:
(千米/小時(shí))滿足下列關(guān)系:![]() (
(![]() ,
,![]() 是常數(shù)).(行駛中的新能源汽車在剎車時(shí)由于慣性作用,要繼續(xù)往前滑行一段距離才能停下,這段距離叫做剎車距離).如圖是根據(jù)多次對(duì)該新能源汽車的實(shí)驗(yàn)數(shù)據(jù)繪制的剎車距離
是常數(shù)).(行駛中的新能源汽車在剎車時(shí)由于慣性作用,要繼續(xù)往前滑行一段距離才能停下,這段距離叫做剎車距離).如圖是根據(jù)多次對(duì)該新能源汽車的實(shí)驗(yàn)數(shù)據(jù)繪制的剎車距離![]() (米)與該車的車速
(米)與該車的車速![]() (千米/小時(shí))的關(guān)系圖.該新能源汽車銷售公司為滿足市場需求,國慶期間在甲、乙兩地同時(shí)展銷該品牌的新能源汽車,在甲地的銷售利潤(單位:萬元)為
(千米/小時(shí))的關(guān)系圖.該新能源汽車銷售公司為滿足市場需求,國慶期間在甲、乙兩地同時(shí)展銷該品牌的新能源汽車,在甲地的銷售利潤(單位:萬元)為![]() ,在乙地的銷售利潤(單位:萬元)為
,在乙地的銷售利潤(單位:萬元)為![]() ,其中
,其中![]() 為銷售量(單位:輛).
為銷售量(單位:輛).
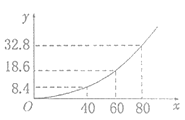
(1)若該公司在兩地共銷售20輛該品牌的新能源汽車,則能獲得的最大利潤![]() 是多少?
是多少?
(2)如果要求剎車距離不超過25.2米,求該品牌新能源汽車行駛的最大速度.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在底面為正方形的四棱錐P-ABCD中,側(cè)棱PD⊥底面ABCD,PD=DC,點(diǎn)E是線段PC的中點(diǎn).

(1)求異面直線AP與BE所成角的大小;
(2)若點(diǎn)F在線段PB上,使得二面角F-DE-B的正弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 的定義城為D,若滿足條件:存在
的定義城為D,若滿足條件:存在![]() ,使
,使![]() 在
在![]() 上的值城為
上的值城為![]() (
(![]() 且
且![]() ),則稱
),則稱![]() 為“k倍函數(shù)”,給出下列結(jié)論:①
為“k倍函數(shù)”,給出下列結(jié)論:①![]() 是“1倍函數(shù)”;②
是“1倍函數(shù)”;②![]() 是“2倍函數(shù)”:③
是“2倍函數(shù)”:③![]() 是“3倍函數(shù)”.其中正確的是( )
是“3倍函數(shù)”.其中正確的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
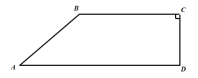
【題目】如圖,某山地車訓(xùn)練中心有一直角梯形森林區(qū)域![]() ,其四條邊均為道路,其中
,其四條邊均為道路,其中![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,
千米,![]() 千米.現(xiàn)有甲、乙兩名特訓(xùn)隊(duì)員進(jìn)行野外對(duì)抗訓(xùn)練,要求同時(shí)從
千米.現(xiàn)有甲、乙兩名特訓(xùn)隊(duì)員進(jìn)行野外對(duì)抗訓(xùn)練,要求同時(shí)從![]() 地出發(fā)勻速前往
地出發(fā)勻速前往![]() 地,其中甲的行駛路線是
地,其中甲的行駛路線是![]() ,速度為
,速度為![]() 千米/小時(shí),乙的行駛路線是
千米/小時(shí),乙的行駛路線是![]() ,速度為
,速度為![]() 千米/小時(shí).
千米/小時(shí).
(1)若甲、乙兩名特訓(xùn)隊(duì)員到達(dá)![]() 地的時(shí)間相差不超過
地的時(shí)間相差不超過![]() 分鐘,求乙的速度
分鐘,求乙的速度![]() 的取值范圍;
的取值范圍;
(2)已知甲、乙兩名特訓(xùn)隊(duì)員攜帶的無線通訊設(shè)備有效聯(lián)系的最大距離是![]() 千米.若乙先于甲到達(dá)
千米.若乙先于甲到達(dá)![]() 地,且乙從
地,且乙從![]() 地到
地到![]() 地的整個(gè)過程中始終能用通訊設(shè)備對(duì)甲保持有效聯(lián)系,求乙的速度
地的整個(gè)過程中始終能用通訊設(shè)備對(duì)甲保持有效聯(lián)系,求乙的速度![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2014年12月19日,2014年中國數(shù)學(xué)奧林匹克競賽(第30屆全國中學(xué)生數(shù)學(xué)冬令營)在重慶市巴蜀中學(xué)舉行.參加本屆中國數(shù)學(xué)奧林匹克競賽共有來自各省、市(自治區(qū)、直轄市)、香港地區(qū)、澳門地區(qū),以及俄羅斯、新加坡等國的30余支代表隊(duì),共317名選手.競賽為期2天,每天3道題,限時(shí)4個(gè)半小時(shí)完成.部分優(yōu)勝者將參加為國際數(shù)學(xué)奧林匹克競賽而組建的中國國家集訓(xùn)隊(duì).中國數(shù)學(xué)奧林匹克競賽(全國中學(xué)生數(shù)學(xué)冬令營)是在全國高中數(shù)學(xué)聯(lián)賽基礎(chǔ)上進(jìn)行的一次較高層次的數(shù)學(xué)競賽,該項(xiàng)活動(dòng)也是中國中學(xué)生級(jí)別最高、規(guī)模最大、最有影響的全國性數(shù)學(xué)競賽.2020年第29屆全國中學(xué)生生物學(xué)競賽也將在重慶巴蜀中學(xué)舉行.巴蜀中學(xué)校本選修課“數(shù)學(xué)建模”興趣小組調(diào)查了2019年參加全國生物競賽的200名學(xué)生(其中男生、女生各100人)的成績,得到這200名學(xué)生成績的中位數(shù)為78.這200名學(xué)生成績均在50與110之間,且成績?cè)?/span>![]() 內(nèi)的人數(shù)為30,這200名學(xué)生成績的高于平均數(shù)的男生有62名,女生有38名.并根據(jù)調(diào)查結(jié)果畫出如圖所示的頻率分布直方圖.
內(nèi)的人數(shù)為30,這200名學(xué)生成績的高于平均數(shù)的男生有62名,女生有38名.并根據(jù)調(diào)查結(jié)果畫出如圖所示的頻率分布直方圖.
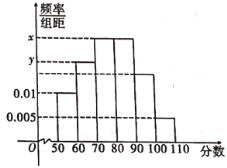
(1)求![]() ,
,![]() 的值;
的值;
(2)填寫下表,能否有![]() 的把握認(rèn)為學(xué)生成績是否高于平均數(shù)與性別有關(guān)系?
的把握認(rèn)為學(xué)生成績是否高于平均數(shù)與性別有關(guān)系?
男生 | 女生 | 總計(jì) | |
成績不高于平均數(shù) | |||
成績高于平均數(shù) | |||
總計(jì) |
參考公式及數(shù)據(jù):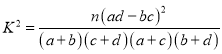 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 是橢圓
是橢圓![]() 上的點(diǎn),
上的點(diǎn),![]() ,
,![]() 是焦點(diǎn),離心率
是焦點(diǎn),離心率![]() .
.
(1)求橢圓的方程;
(2)設(shè)![]() ,
,![]() 是橢圓上的兩點(diǎn),且
是橢圓上的兩點(diǎn),且![]() ,(
,(![]() 是定數(shù)),問線段
是定數(shù)),問線段![]() 的垂直平分線是否過定點(diǎn)?若過定點(diǎn),求出此定點(diǎn)的坐標(biāo),若不存在,說明理由.
的垂直平分線是否過定點(diǎn)?若過定點(diǎn),求出此定點(diǎn)的坐標(biāo),若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
,![]() ,
,![]() .
.
(1)當(dāng)![]() ,
,![]() ,求曲線
,求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最小值為
上的最小值為![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值;
的值;
(3)當(dāng)![]() 時(shí),若函數(shù)
時(shí),若函數(shù)![]() 恰有兩個(gè)零點(diǎn)
恰有兩個(gè)零點(diǎn)![]() ,
,![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com