【題目】為了政府對過熱的房地產(chǎn)市場進行調(diào)控決策，統(tǒng)計部門對城市人和農(nóng)村人進行了買房的心理預期調(diào)研，用簡單隨機抽樣的方法抽取110人進行統(tǒng)計，得到如下列聯(lián)表：
買房 | 不買房 | 糾結(jié) | |
城市人 | 5 | 15 | |
農(nóng)村人 | 20 | 10 |
已知樣本中城市人數(shù)與農(nóng)村人數(shù)之比是3：8．
分別求樣本中城市人中的不買房人數(shù)和農(nóng)村人中的糾結(jié)人數(shù)；
用獨立性檢驗的思想方法說明在這三種買房的心理預期中哪一種與城鄉(xiāng)有關？
參考公式：
．
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
【答案】（1）樣本中城市人中的不買房人數(shù)為10人，農(nóng)村人中的糾結(jié)人數(shù)為50人；（2）有
的把握認為不買房與城鄉(xiāng)有關.
【解析】
設城市人中的不買房人數(shù)為x，農(nóng)村人中的糾結(jié)人數(shù)為y，根據(jù)題意列出方程組求解即可；
設三種心理障礙都與性別無關，由得到列聯(lián)表，對于上述三種心理障礙分別構(gòu)造三個隨機變量
，
，
；由表中數(shù)據(jù)計算、和的值，對照數(shù)表得出結(jié)論．
解：設城市人中的不買房人數(shù)為x，農(nóng)村人中的糾結(jié)人數(shù)為y，
則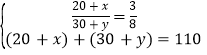
，
解得
；
樣本中城市人中的不買房人數(shù)為10人，農(nóng)村人中的糾結(jié)人數(shù)為50人；
設三種心理障礙都與性別無關，由得到列聯(lián)表如下；
買房 | 不買房 | 糾結(jié) | 總計 | |
城市人 | 5 | 10 | 15 | 30 |
農(nóng)村人 | 20 | 10 | 50 | 85 |
總計 | 25 | 20 | 65 | 110 |
對于上述三種心理障礙分別構(gòu)造三個隨機變量，，；
由表中數(shù)據(jù)可得
；
；
；
所以，沒有充分的證明顯示買房與城鄉(xiāng)有關，
有的把握認為不買房與城鄉(xiāng)有關，
沒有充分的證明顯示糾結(jié)與城鄉(xiāng)有關．
科目：高中數(shù)學 來源： 題型：
【題目】已知某校5個學生的數(shù)學和物理成績?nèi)缦拢?/span>
學生的編號 | 1 | 2 | 3 | 4 | 5 |
數(shù)學成績 | 80 | 75 | 70 | 65 | 60 |
物理成績 | 70 | 66 | 68 | 64 | 62 |
（1）通過大量事實證明發(fā)現(xiàn)，一個學生的數(shù)學成績和物理成績是具有很強的線性相關關系的，在上述表格中，用
表示數(shù)學成績，用
表示物理成績，求關于的回歸方程．
（2）利用殘差分析回歸方程的擬合效果，若殘差和在
范圍內(nèi)，則稱回歸方程為“優(yōu)擬方程”，問：該回歸方程是否為“優(yōu)擬方程”．
（3）現(xiàn)從5名同學中任選兩人參加訪談活動，求1號同學沒被選中的概率.
附：對于一組數(shù)據(jù)
，
，…，
，其回歸直線
的斜率和截距的最小二乘估計分別為：
，
.
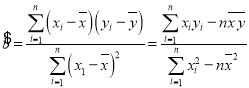查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在直角坐標系
中，以
為極點，
軸的正半軸為極軸建立極坐標系，已知曲線
的極坐標方程為
，曲線
的極坐標方程為
，曲線
的極坐標方程為
.
（1）求與的直角坐標方程；
（2）若與的交于
點，與交于
、
兩點，求
的面積.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】正方體
的棱長為
， 
為
的中點， 
為線段
的動點，過
的平面截該正方體所得的截面記為
，則下列命題正確的序號是_________.
①當
時， 
的面積為
；
②當
時， 
為六邊形；
③當
時， 
與
的交點
滿足
；
④當
時， 
為等腰梯形；
⑤當
時， 
為四邊形.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在某公司舉行的年終慶典活動中，主持人利用隨機抽獎軟件進行抽獎：由電腦隨機生成一張如圖所示的3
3表格，其中1格設獎300元，4格各設獎200元，其余4格各設獎100元，點擊某一格即顯示相應金額．某人在一張表中隨機不重復地點擊3格，記中獎的總金額為X元．
（1）求概率
；
（2）求
的概率分布及數(shù)學期望
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在四棱錐
中，側(cè)面
底面ABCD，底面ABCD為直角梯形，
，
，
，
，E，F分別為AD，PC的中點．
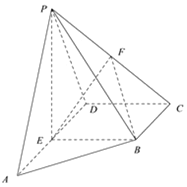
Ⅰ
求證：
平面BEF；
Ⅱ若
，求二面角
的余弦值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
（其中
，
為自然對數(shù)的底數(shù)，
）.
（1）若
，求函數(shù)
的單調(diào)區(qū)間；
（2）證明：當
時，函數(shù)有兩個零點
，且
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
