
【題目】已知向量![]() = (1,2sinθ),
= (1,2sinθ),![]() = (sin(θ+
= (sin(θ+![]() ),1),θ
),1),θ![]() R。
R。
(1) 若![]() ⊥
⊥![]() ,求 tanθ的值;
,求 tanθ的值;
(2) 若![]() ∥
∥![]() ,且 θ
,且 θ![]() (0,
(0,![]() ),求 θ的值
),求 θ的值
【答案】(1)tanθ=-![]() ;(2)θ=
;(2)θ=![]() .
.
【解析】
(1)利用兩個向量垂直的坐標表示,列出方程,化簡可求得![]() 的值.(2)利用兩個向量平行的坐標表示,列出方程,化簡可求得
的值.(2)利用兩個向量平行的坐標表示,列出方程,化簡可求得![]() 的值.
的值.
(1)依題意,得:![]()
![]() =0,即
=0,即
sin(θ+![]() )+2sinθ=0,展開,得:
)+2sinθ=0,展開,得:
sinθcos![]() +cosθsin
+cosθsin![]() +2sinθ=0,
+2sinθ=0,
化簡,得:![]() sinθ+
sinθ+![]() cosθ=0,解得:tanθ=-
cosθ=0,解得:tanθ=-![]()
(2)因為![]() ∥
∥![]() ,所以,2sinθsin(θ+
,所以,2sinθsin(θ+![]() )=1,展開得:
)=1,展開得:
2sinθ(sinθcos![]() +cosθsin
+cosθsin![]() )=1,
)=1,
即:2sin2θ+2![]() sinθcosθ=2,
sinθcosθ=2,
即:1-cos2θ+![]() sin2θ=2,
sin2θ=2,
化為:sin(2θ-![]() )=
)=![]() ,因為θ
,因為θ![]() (0,
(0,![]() ),所以,2θ-
),所以,2θ-![]()
![]() (
(![]() ),
),
所以,2θ-![]() =
=![]() ,解得:θ=
,解得:θ=![]()


科目:高中數學 來源: 題型:
【題目】峰谷電是目前在城市居民當中開展的一種電價類別.它是將一天24小時劃分成兩個時間段,把8:00—22:00共14小時稱為峰段,執行峰電價,即電價上調;22:00—次日8:00共10個小時稱為谷段,執行谷電價,即電價下調.為了進一步了解民眾對峰谷電價的使用情況,從某市一小區隨機抽取了50 戶住戶進行夏季用電情況調查,各戶月平均用電量以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:度)分組的頻率分布直方圖如下圖:
(單位:度)分組的頻率分布直方圖如下圖:

若將小區月平均用電量不低于700度的住戶稱為“大用戶”,月平均用電量低于700度的住戶稱為“一般用戶”.其中,使用峰谷電價的戶數如下表:
月平均用電量(度) |
|
|
|
|
|
|
使用峰谷電價的戶數 | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估計所抽取的 50戶的月均用電量的眾數和平均數(同一組中的數據用該組區間的中點值作代表);
(2)(![]() )將“一般用戶”和“大用戶”的戶數填入下面
)將“一般用戶”和“大用戶”的戶數填入下面![]() 的列聯表:
的列聯表:
一般用戶 | 大用戶 | |
使用峰谷電價的用戶 | ||
不使用峰谷電價的用戶 |
(![]() )根據(
)根據(![]() )中的列聯表,能否有
)中的列聯表,能否有![]() 的把握認為 “用電量的高低”與“使用峰谷電價”有關?
的把握認為 “用電量的高低”與“使用峰谷電價”有關?
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附:![]() ,
,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電視臺為宣傳本市,隨機對本市內![]() 歲的人群抽取了
歲的人群抽取了![]() 人,回答問題“本市內著名旅游景點有哪些” ,統計結果如圖表所示.
人,回答問題“本市內著名旅游景點有哪些” ,統計結果如圖表所示.
組號 | 分組 | 回答正確的人數 | 回答正確的人數占本組的頻率 |
第1組 | [15,25) | a | 0.5 |
第2組 | [25,35) | 18 | x |
第3組 | [35,45) | b | 0.9 |
第4組 | [45,55) | 9 | 0.36 |
第5組 | [55,65] | 3 | y |

(1)分別求出![]() 的值;
的值;
(2)根據頻率分布直方圖估計這組數據的中位數(保留小數點后兩位)和平均數;
(3)若第1組回答正確的人員中,有2名女性,其余為男性,現從中隨機抽取2人,求至少抽中1名女性的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
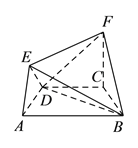
(![]() )求證:
)求證: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在線段
)在線段![]() (含端點)上,是否存在一點
(含端點)上,是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(![]() )見解析;(
)見解析;(![]() )
)![]() ;(
;(![]() )存在,
)存在, ![]()
【解析】試題分析:(1)由題意,證明![]() ,
, ![]() ,證明
,證明![]() 面
面![]() ;(2)建立空間直角坐標系,求平面
;(2)建立空間直角坐標系,求平面![]() 和平面
和平面![]() 的法向量,解得余弦值為
的法向量,解得余弦值為![]() ;(3)得
;(3)得![]() ,
, 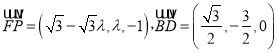 ,所以
,所以![]() ,
, ![]() ,所以存在
,所以存在![]() 為
為![]() 中點.
中點.
試題解析:
(![]() )∵
)∵![]() ,
, ![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() .
.
∵![]() ,且
,且![]() ,
,
![]() 、
、![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(![]() )知
)知![]() ,∴
,∴![]() .
.
∵![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 兩兩垂直,以
兩兩垂直,以![]() 為坐標原點,
為坐標原點,
以![]() ,
, ![]() ,
, ![]() 為
為![]() ,
, ![]() ,
, ![]() 軸建系.
軸建系.
設![]() ,則
,則![]() ,
, ![]() ,
,  ,
, ![]() ,
, ![]() ,
,
∴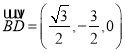 ,
, ![]() .
.
設![]() 的一個法向量為
的一個法向量為![]() ,
,
∴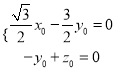 ,取
,取![]() ,則
,則![]() .
.
由于![]() 是面
是面![]() 的法向量,
的法向量,
則 .
.
∵二面角![]() 為銳二面角,∴余弦值為
為銳二面角,∴余弦值為![]() .
.
(![]() )存在點
)存在點![]() .
.
設![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 面
面![]() ,
, 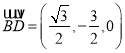 .
.
若![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴存在
,∴存在![]() 為
為![]() 中點.
中點.

【題型】解答題
【結束】
19
【題目】已知函數![]() .
.
(![]() )當
)當![]() 時,求此函數對應的曲線在
時,求此函數對應的曲線在![]() 處的切線方程.
處的切線方程.
(![]() )求函數
)求函數![]() 的單調區間.
的單調區間.
(![]() )對
)對![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 為偶函數,且當
為偶函數,且當![]() 時,
時,![]() .記
.記![]() .給出下列關于函數
.給出下列關于函數![]() 的說法:①當
的說法:①當![]() 時,
時,![]() ;②函數
;②函數![]() 為奇函數;③函數
為奇函數;③函數![]() 在
在![]() 上為增函數;④函數
上為增函數;④函數![]() 的最小值為
的最小值為![]() ,無最大值.其中正確的是______.
,無最大值.其中正確的是______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com