
【題目】交強險是車主須為機動車購買的險種.若普通![]() 座以下私家車投保交強險第一年的費用(基本保費)是
座以下私家車投保交強險第一年的費用(基本保費)是![]() 元,在下一年續保時,實行費率浮動制,其保費與上一年度車輛發生道路交通事故情況相聯系,具體浮動情況如下表:
元,在下一年續保時,實行費率浮動制,其保費與上一年度車輛發生道路交通事故情況相聯系,具體浮動情況如下表:
類型 | 浮動因素 | 浮動比率 |
| 上一年度未發生有責任的道路交通事故 | 下浮 |
| 上兩年度未發生有責任的道路交通事故 | 下浮 |
| 上三年度未發生有責任的道路交通事故 | 下浮 |
| 上一年度發生一次有責任不涉及死亡的道路交通事故 |
|
| 上一年度發生兩次及以上有責任不涉及死亡的道路交通事故 | 上浮 |
| 上三年度發生有責任涉及死亡的道路交通事故 | 上浮 |
某一機構為了研究某一品牌![]() 座以下投保情況,隨機抽取了
座以下投保情況,隨機抽取了![]() 輛車齡滿三年的該品牌同型號私家車的下一年續保情況,統計得到如下表格:
輛車齡滿三年的該品牌同型號私家車的下一年續保情況,統計得到如下表格:
類型 |
|
|
|
|
|
|
數量 |
|
|
|
|
|
|
以這![]() 輛該品牌汽車的投保類型的頻率視為概率.
輛該品牌汽車的投保類型的頻率視為概率.
(I)試估計該地使用該品牌汽車的一續保人本年度的保費不超過![]() 元的概率;
元的概率;
(II)記![]() 為某家庭的一輛該品牌車在第四年續保時的費用,求
為某家庭的一輛該品牌車在第四年續保時的費用,求![]() 的分布列和期望.
的分布列和期望.
 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:高中數學 來源: 題型:
【題目】一個棱柱是正四棱柱的充要條件是( )
A.底面是正方形,有兩個側面是矩形B.底面是正方形,有兩個側面垂直底面
C.底面是正方形,相鄰兩個側面是矩形D.每個側面都是全等的矩形
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設過點![]() 且傾斜角為
且傾斜角為![]() 的直線
的直線![]() 和曲線
和曲線![]() 交于兩點
交于兩點![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面內與兩定點![]() ,
,![]() 連線的斜率之積等于非零常數
連線的斜率之積等于非零常數![]() 的點的軌跡,加上
的點的軌跡,加上![]() 、
、![]() 兩點所成的曲線
兩點所成的曲線![]() 可以是圓、橢圓或雙曲線,給出以下四個結論:①當
可以是圓、橢圓或雙曲線,給出以下四個結論:①當![]() 時,曲線
時,曲線![]() 是一個圓;②當
是一個圓;②當![]() 時,曲線
時,曲線![]() 的離心率為
的離心率為![]() ;③當
;③當![]() 時,曲線
時,曲線![]() 的漸近線方程為
的漸近線方程為![]() ;④當曲線
;④當曲線![]() 的焦點坐標分別為
的焦點坐標分別為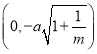 和
和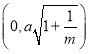 時,
時,![]() 的范圍是
的范圍是![]() .其中正確的結論序號為_______.
.其中正確的結論序號為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數且
為參數且 ![]() )曲線
)曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,且
為參數,且![]() ),以
),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為:
的極坐標方程為:![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 與
與![]() 的交點到極點的距離;
的交點到極點的距離;
(2)設![]() 與
與![]() 交于
交于![]() 點,
點,![]() 與
與![]() 交于
交于![]() 點,當
點,當![]() 在
在![]() 上變化時,求
上變化時,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在棱長為1的正方體![]() 中,點
中,點![]() 是對角線
是對角線![]() 上的動點(點
上的動點(點![]() 與
與![]() 不重合),則下列結論正確的是__________
不重合),則下列結論正確的是__________
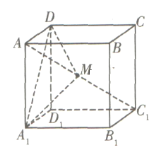
①存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
③![]() 的面積可能等于
的面積可能等于![]() ;
;
④若![]() 分別是
分別是![]() 在平面
在平面![]() 與平面
與平面![]() 的正投影的面積,則存在點
的正投影的面積,則存在點![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直角坐標系xOy中,圓O:x2+y2=4與x軸負半軸交于點A,過點A的直線AM,AN分別與圓O交于M,N兩點,設直線AM、AN的斜率分別為k1、k2.
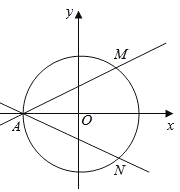
(1)若![]() ,求△AMN的面積;
,求△AMN的面積;
(2)若k1k2=-2,求證:直線MN過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com