【題目】如果四面體的四條高交于一點，則該點稱為四面體的垂心，該四面體稱為垂心四面體.
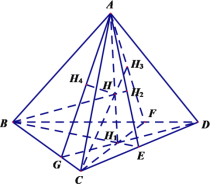
（1）證明：如果四面體的對棱互相垂直，則該四面體是垂心四面體；反之亦然.
（2）給出下列四面體
①正三棱錐；
②三條側(cè)棱兩兩垂直；
③高在各面的射影過所在面的垂心；
④對棱的平方和相等.
其中是垂心四面體的序號為 .
【答案】（1）證明見解析（2）①②③④
【解析】
（1）首先證明四面體的兩條高線交于一點，再證過另一頂點和這一點的直線為另一條高線，即可證明結(jié)論成立.（2）①②③可通過證明對棱垂直證明是垂心四面體，④假設(shè)四面體為垂心四面體，則可證明有對棱的平方和相等，逆推依然成立，所以④也成立.
（1）先證對棱互相垂直的四面體是垂心四面體.
作
，則
，
此時兩條高線
連接
，下證
.連接
綜上可知，四條高線交于點
，故該四面體為垂心四面體；
反之，若該四面體為垂心四面體，即四條高線交于點.
,
,
，故
,
同理可證
（2）①正三棱錐底面為正三角形，側(cè)面為全等的等腰三角形，可證明三組對棱兩兩垂直，所以①符合要求.②三條側(cè)棱兩兩垂直，任一條側(cè)棱垂直另外兩條側(cè)棱所在的平面，也可證明對棱垂直，所以②符合要求.③高垂直于底面棱，在側(cè)面的射影垂直于此面的底面棱，所以底面棱垂直于高和射影所在的平面，即垂直于對棱，所以③符合要求.④假設(shè)四面體
為垂心四面體，設(shè)BF交CD于E，則AC2﹣AD2＝CF2﹣DF2＝CE2﹣DE2＝BC2﹣BD2，即AC2+BD2＝AD2+BC2，反之，若故AC2+BD2＝AD2+BC2，則有C2﹣AD2＝CF2﹣DF2＝CE2﹣DE2＝BC2﹣BD2成立，即
同理可證其他，故④符合要求．
①②③④均符合要求.
天天向上一本好卷系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知橢圓
的離心率是
，一個頂點是
．
（Ⅰ）求橢圓
的方程；
（Ⅱ）設(shè)
，
是橢圓上異于點
的任意兩點，且
．試問：直線
是否恒過一定點？若是，求出該定點的坐標；若不是，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知拋物線C：x2=2py經(jīng)過點（2，1）．
（Ⅰ）求拋物線C的方程及其準線方程；
（Ⅱ）設(shè)O為原點，過拋物線C的焦點作斜率不為0的直線l交拋物線C于兩點M，N，直線y=1分別交直線OM，ON于點A和點B.求證：以AB為直徑的圓經(jīng)過y軸上的兩個定點．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某班從4位男生和3位女生志愿者選出4人參加校運會的點名簽到工作，則選出的志愿者中既有男生又有女生的概率的是__________.（結(jié)果用最簡分數(shù)表示）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】我們稱滿足以下兩個條件的有窮數(shù)列
為
階“期待數(shù)列”；①
；②
.
（1）若數(shù)列
的通項公式是
，試判斷數(shù)列是否為2014階“期待數(shù)列”，并說明理由；
（2）若等比數(shù)列
為
階“期待數(shù)列”，求公比
及數(shù)列的通項公式；
（3）若一個等差數(shù)列
既是（）階“期待數(shù)列”又是遞增數(shù)列，求該數(shù)列的通項公式.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知關(guān)于x的一元二次不等式ax2+x+b＞0的解集為（-∞，-2）∪（1，+∞）．
（Ⅰ）求a和b的值；
（Ⅱ）求不等式ax2-（c+b）x+bc＜0的解集．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在四棱錐PABCD中，AD∥BC，平面PAC⊥平面ABCD，AB=AD=DC=1，
∠ABC=∠DCB=60，E是PC上一點.
（Ⅰ）證明：平面EAB⊥平面PAC；
（Ⅱ）若△PAC是正三角形，且E是PC中點，求三棱錐AEBC的體積.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】拋物線
的焦點為F，圓
，點
為拋物線上一動點.已知當
的面積為
.
（I）求拋物線方程；
（II）若
，過P做圓C的兩條切線分別交y軸于M，N兩點，求
面積的最小值，并求出此時P點坐標.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】高一年級某個班分成8個小組，利用假期參加社會公益服務(wù)活動
每個小組必須全員參加
，參加活動的次數(shù)記錄如下：
組別 |
|
|
|
|
|
|
|
|
參加活動次數(shù) | 3 | 2 | 4 | 3 | 2 | 4 | 1 | 3 |
Ⅰ從這8個小組中隨機選出2個小組在全校進行活動匯報
求“選出的2個小組參加社會公益服務(wù)活動次數(shù)相等”的概率；
Ⅱ記每個小組參加社會公益服務(wù)活動的次數(shù)為X．
求X的分布列和數(shù)學(xué)期望EX；
至
幾小組每組有4名同學(xué)，
小組有5名同學(xué)記“該班學(xué)生參加社會公益服務(wù)活動的平均次數(shù)”為
，寫出與EX的大小關(guān)系結(jié)論不要求證明．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
