
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實數(shù)
,求實數(shù)![]() 的值;
的值;
(2)設![]() ,若對任意兩個不等的正數(shù)
,若對任意兩個不等的正數(shù)![]() ,
,![]() ,都有
,都有![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若在![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)借助題設條件運用導數(shù)的幾何意義建立方程求解;(2)借助題設運用轉(zhuǎn)化化歸的思想進行轉(zhuǎn)化再運用導數(shù)知識求解;(3)依據(jù)題設先將問題進行轉(zhuǎn)化,再借助導數(shù)知識分類整合思想分類探求求解.
試題解析:
(1)由![]()
![]() ,得
,得![]() ,
,
由題意![]() ,所以
,所以![]() .
.
(2)![]() ,
,
因為對任意兩個不等的正數(shù)![]() ,
,![]() ,都有
,都有![]() ,
,
設![]() ,則
,則![]() ,即
,即![]() 恒成立,
恒成立,
問題等價于函數(shù)![]() ,即
,即![]() 在
在![]() 為增函數(shù),
為增函數(shù),
所以![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() ,即實數(shù)
,即實數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.
(3)不等式![]() 等價于
等價于![]() ,
,
整理得![]() ,
,
設![]() ,由題意知,在
,由題意知,在![]() 上存在一點
上存在一點![]() ,使得
,使得![]() ,
,
由![]() ,
,
因為![]() ,所以
,所以![]() ,令
,令![]() ,得
,得![]() .
.
①當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
只需![]() ,解得
,解得![]() .
.
②當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 處取最小值,
處取最小值,
令![]() ,即
,即![]() ,可得
,可得![]() ,
,
考查式子![]() ,因為
,因為![]() ,可得左端大于1,而右端小于1,所以不等式不可能成立.
,可得左端大于1,而右端小于1,所以不等式不可能成立.
③當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
只需![]() ,解得
,解得![]() .
.
綜上所述,實數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】 “中國式過馬路”是網(wǎng)友對部分中國人集體闖紅燈現(xiàn)象的一種調(diào)侃,即“湊夠一撮人就可以走了,和紅綠燈無關.”出現(xiàn)這種現(xiàn)象是大家受法不責眾的“從眾”心理影響,從而不顧及交通安全.某校對全校學生過馬路方式進行調(diào)查,在所有參與調(diào)查的人中,“跟從別人闖紅燈”“從不闖紅燈”“帶頭闖紅燈”人數(shù)如表所示:
跟從別人闖紅燈 | 從不闖紅燈 | 帶頭闖紅燈 | |
男生 | 800 | 450 | 200 |
女生 | 100 | 150 | 300 |
(Ⅰ)在所有參與調(diào)查的人中,用分層抽樣的方法抽取n人,已知“跟從別人闖紅燈”的人抽取了45 人,求n的值;
(Ⅱ)在“帶頭闖紅燈”的人中,將男生的200人編號為1,2,…,200;將女生的300人編號為201,202,…,500,用系統(tǒng)抽樣的方法抽取4人參加“文明交通”宣傳活動,若抽取的第一個人的編號為100,把抽取的4人看成一個總體,從這4人中任選取2人,求這兩人均是女生的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某大學餐飲中心為了了解新生的飲食習慣,利用簡單隨機抽樣的方法在全校一年級學生中進行了抽樣調(diào)查,調(diào)查結果如下表所示:
喜歡甜品 | 不喜歡甜品 | 合計 | |
南方學生 | 60 | 20 | 80 |
北方學生 | 10 | 10 | 20 |
合計 | 70 | 30 | 100 |
(1)根據(jù)表中數(shù)據(jù),問是否有95%的把握認為“南方學生和北方學生在選用甜品的飲食習慣方面有差異”;
(2)根據(jù)(1)的結論,你能否提出更好的調(diào)查方法來了解該校大學新生的飲食習慣,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立的極坐標系中,直線
軸的非負半軸為極軸建立的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ),曲線
),曲線![]() 的參數(shù)方程為
的參數(shù)方程為
(1)寫出直線![]() 及曲線
及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)過點![]() 平行于直線
平行于直線![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() ,求點
,求點![]() 軌跡的直角坐標方程.
軌跡的直角坐標方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,在四棱錐![]() 中,四邊形
中,四邊形![]() 為矩形,△
為矩形,△![]() 為等腰三角形,
為等腰三角形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.

(1)證明:![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() ;
;
(3)求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,游客從某旅游景區(qū)的景點![]() 處下上至
處下上至![]() 處有兩種路徑.一種是從
處有兩種路徑.一種是從![]() 沿直線步行到
沿直線步行到![]() ,另一種是先從
,另一種是先從![]() 沿索道乘纜車到
沿索道乘纜車到![]() ,然后從
,然后從![]() 沿直線步行到
沿直線步行到![]() .現(xiàn)有甲、乙兩位游客從
.現(xiàn)有甲、乙兩位游客從![]() 處下山,甲沿
處下山,甲沿![]() 勻速步行,速度為
勻速步行,速度為![]() .在甲出發(fā)
.在甲出發(fā)![]() 后,乙從
后,乙從![]() 乘纜車到
乘纜車到![]() ,在
,在![]() 處停留
處停留![]() 后,再從
后,再從![]() 勻速步行到
勻速步行到![]() ,假設纜車勻速直線運動的速度為
,假設纜車勻速直線運動的速度為![]() ,山路
,山路![]() 長為1260
長為1260![]() ,經(jīng)測量
,經(jīng)測量![]() ,
,![]() .
.

(1)求索道![]() 的長;
的長;
(2)問:乙出發(fā)多少![]() 后,乙在纜車上與甲的距離最短?
后,乙在纜車上與甲的距離最短?
(3)為使兩位游客在![]() 處互相等待的時間不超過
處互相等待的時間不超過![]() ,乙步行的速度應控制在什么范圍內(nèi)?
,乙步行的速度應控制在什么范圍內(nèi)?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,ABCD是塊矩形硬紙板,其中AB=2AD,AD=![]() ,E為DC的中點,將它沿AE折成直二面角D-AE-B.
,E為DC的中點,將它沿AE折成直二面角D-AE-B.
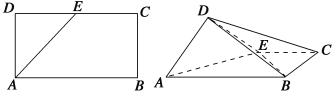
(1)求證:AD⊥平面BDE;
(2)求二面角B-AD-E的余弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com