
【題目】已知![]() .
.
(1)求![]() 的定義域;并證明
的定義域;并證明![]() 是定義域上的奇函數;
是定義域上的奇函數;
(2)判斷![]() 在定義域上的單調性(無需證明);
在定義域上的單調性(無需證明);
(3)求使不等式![]() 解集.
解集.
科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,平面
中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為正方形,四邊形
為正方形,四邊形![]() 為梯形,且
為梯形,且![]() ,
,![]() ,
,![]() .
.
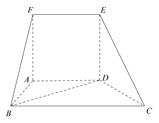
(1)求證:![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】5名男生3名女生參加升旗儀式:
(1)站兩橫排,3名女生站前排,5名男生站后排有多少種站法?
(2)站兩縱列,每列4人,每列都有女生且女生站在男生前面,有多少種排列方法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是平行四邊形,
是平行四邊形,![]() ,
,![]() 為
為![]() 的中點,且有
的中點,且有![]() ,現以
,現以![]() 為折痕,將
為折痕,將![]() 折起,使得點
折起,使得點![]() 到達點
到達點![]() 的位置,且
的位置,且![]()
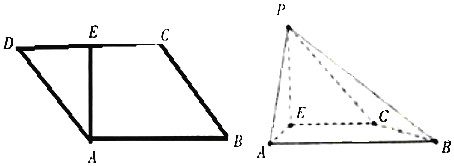
(1)證明:![]() 平面
平面![]() ;
;
(2)若四棱錐![]() 的體積為
的體積為![]() ,求四棱錐
,求四棱錐![]() 的側面積.
的側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】棱長為1的正方體![]() 中,點
中,點![]() 、
、![]() 分別在線段
分別在線段![]() 、
、![]() 上運動(不包括線段端點),且
上運動(不包括線段端點),且![]() .以下結論:①
.以下結論:①![]() ;②若點
;②若點![]() 、
、![]() 分別為線段
分別為線段![]() 、
、![]() 的中點,則由線
的中點,則由線![]() 與
與![]() 確定的平面在正方體
確定的平面在正方體![]() 上的截面為等邊三角形;③四面體
上的截面為等邊三角形;③四面體![]() 的體積的最大值為
的體積的最大值為![]() ;④直線
;④直線![]() 與直線
與直線![]() 的夾角為定值.其中正確的結論為______.(填序號)
的夾角為定值.其中正確的結論為______.(填序號)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,
,![]() ,
,![]() 分別是其左、右焦點,且過點
分別是其左、右焦點,且過點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若在直線![]() 上任取一點
上任取一點![]() ,從點
,從點![]() 向
向![]() 的外接圓引一條切線,切點為
的外接圓引一條切線,切點為![]() .問是否存在點
.問是否存在點![]() ,恒有
,恒有![]() ?請說明理由.
?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com